2021 CryptoCTF

Van1sh 比赛小屋
创建时间:
字数:19.6k 阅读:
  1. Farm
  2. Keybase
  3. Rima
  4. Titu
  5. Symbols
  6. Hyper Normal
  7. Salt and Pepper
  8. Hamul
  9. Triplet
  10. Onlude
  11. Maid
  12. Wolf
  13. Ferman
  14. RSAphantine
  15. FROZEN
  16. LINDA
  17. TinyECC
  18. ELEGANT CURVE
  19. DOUBLE MIFF
  20. ECCHIMERA
  21. ROHALD
  22. ROBERT
  23. TRUNC
  24. MY SIEVE
  25. DORSA
  26. POLISH
1
2
3
4
5
6
7
Crypto CTF is an online competition for hackers to test, evaluate, and expand their cryptography exploiting skills. In this CTF, we will provide various crypto challenges regarding modern cryptography techniques.
All crypto lovers are most welcome!
Crypto CTF is a revenge for everlasting complaints by CTF participants about crypto challenges in CTF contests. In this brand-new tournament, we are trying to provide the crypto lovers with fun and challenging pure crypto tasks to squeeze their heart and test their passion for cryptography.
Each task will be based on a particular cryptographic primitive, or it will include a direct application of cryptography in other fields.
The organizers of these tournaments generously offer their skills' knowledge to design original Crypto tasks and challenges for similar contests.

Long Live Crypto :)

这两天在复现2022-CryptoCTF，但是想着2021的CryptoCTF也没复现完，于是就决定先从2021开始了。

Farm

POINTS：41

考点：有限域，逐字节爆破

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#!/usr/bin/env sage

from sage.all import *
import string, base64, math
from flag import flag

ALPHABET = string.printable[:62] + '\\='

F = list(GF(64))

def keygen(l):
	key = [F[randint(1, 63)] for _ in range(l)] 
	key = math.prod(key) # Optimization the key length :D
	return key

def maptofarm(c):
	assert c in ALPHABET
	return F[ALPHABET.index(c)]

def encrypt(msg, key):
	m64 = base64.b64encode(msg)
	enc, pkey = '', key**5 + key**3 + key**2 + 1
	for m in m64:
		enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
	return enc

# KEEP IT SECRET 
key = keygen(14) # I think 64**14 > 2**64 is not brute-forcible :P

enc = encrypt(flag, key)
print(f'enc = {enc}')

#enc = "805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj"

这道题目，生成了一个F = list(GF(64))，这里用sagemath测试一下，得到的是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
[0,
 z6,
 z6^2,
 z6^3,
 z6^4,
 z6^5,
 z6^4 + z6^3 + z6 + 1,
 z6^5 + z6^4 + z6^2 + z6,
 z6^5 + z6^4 + z6^2 + z6 + 1,
 z6^5 + z6^4 + z6^2 + 1,
 z6^5 + z6^4 + 1,
 z6^5 + z6^4 + z6^3 + 1,
 z6^5 + z6^3 + 1,
 z6^3 + 1,
 z6^4 + z6,
 z6^5 + z6^2,
 z6^4 + z6 + 1,
 z6^5 + z6^2 + z6,
 z6^4 + z6^2 + z6 + 1,
 z6^5 + z6^3 + z6^2 + z6,
 z6^2 + z6 + 1,
 z6^3 + z6^2 + z6,
 z6^4 + z6^3 + z6^2,
 z6^5 + z6^4 + z6^3,
 z6^5 + z6^3 + z6 + 1,
 z6^3 + z6^2 + 1,
 z6^4 + z6^3 + z6,
 z6^5 + z6^4 + z6^2,
 z6^5 + z6^4 + z6 + 1,
 z6^5 + z6^4 + z6^3 + z6^2 + 1,
 z6^5 + 1,
 z6^4 + z6^3 + 1,
 z6^5 + z6^4 + z6,
 z6^5 + z6^4 + z6^3 + z6^2 + z6 + 1,
 z6^5 + z6^2 + 1,
 z6^4 + 1,
 z6^5 + z6,
 z6^4 + z6^3 + z6^2 + z6 + 1,
 z6^5 + z6^4 + z6^3 + z6^2 + z6,
 z6^5 + z6^2 + z6 + 1,
 z6^4 + z6^2 + 1,
 z6^5 + z6^3 + z6,
 z6^3 + z6^2 + z6 + 1,
 z6^4 + z6^3 + z6^2 + z6,
 z6^5 + z6^4 + z6^3 + z6^2,
 z6^5 + z6 + 1,
 z6^4 + z6^3 + z6^2 + 1,
 z6^5 + z6^4 + z6^3 + z6,
 z6^5 + z6^3 + z6^2 + z6 + 1,
 z6^2 + 1,
 z6^3 + z6,
 z6^4 + z6^2,
 z6^5 + z6^3,
 z6^3 + z6 + 1,
 z6^4 + z6^2 + z6,
 z6^5 + z6^3 + z6^2,
 z6 + 1,
 z6^2 + z6,
 z6^3 + z6^2,
 z6^4 + z6^3,
 z6^5 + z6^4,
 z6^5 + z6^4 + z6^3 + z6 + 1,
 z6^5 + z6^3 + z6^2 + 1,
 1]

长度正好是64。ok，虽然不是很明白怎么来的，但是可以先放一边。然后看到程序调用了keygen(l)函数，

1
2
3
4
def keygen(l):
	key = [F[randint(1, 63)] for _ in range(l)] 
	key = math.prod(key) # Optimization the key length :D
	return key

该函数首先生成长度为l的数组，元素取自F，最后prod所有的元素，但由于其结果仍会在F这个galois-field中，所以到这里已经可以预见这道题怎么做了，只用穷举一下这个F中的所有元素当作key即可，只有64种可能。

然后我们看具体的加密流程以编写解密算法。

1
2
3
4
5
6
def encrypt(msg, key):
	m64 = base64.b64encode(msg)
	enc, pkey = '', key**5 + key**3 + key**2 + 1
	for m in m64:
		enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
	return enc

重点在enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]

看到算法是对明文逐位字节加密的，并且根据这个比赛的flag格式，我们知道明文前三个字节应该是‘CCT’，那么也就知道了其base64编码所以，我们可以先爆破出密钥，然后逐字节爆破明文

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import string, base64, math


ALPHABET = string.printable[:62] + '\\='

F = list(GF(64))

def keygen(l):
	key = [F[randint(1, 63)] for _ in range(l)] 
	key = math.prod(key) # Optimization the key length :D
	return key

def maptofarm(c):
	assert c in ALPHABET
	return F[ALPHABET.index(c)]

def encrypt(msg, key):
	m64 = base64.b64encode(msg)
	enc, pkey = '', key**5 + key**3 + key**2 + 1
	for m in m64:
		enc += ALPHABET[F.index(pkey * maptofarm(chr(m)))]
	return enc

def myenc(m,key):
	enc, pkey = '', key**5 + key**3 + key**2 + 1
	enc += ALPHABET[F.index(pkey * maptofarm(m))]
	return enc

flag = b'CCT'
flag64 = b''
ciphertext = '805c9GMYuD5RefTmabUNfS9N9YrkwbAbdZE0df91uCEytcoy9FDSbZ8Ay8jj'
for key in F:
	if encrypt(flag,key) == ciphertext[:4]:
		for i in ciphertext:
			for j in ALPHABET:
				if myenc(j,key) == i:
					flag64+=j.encode()
					break
print(base64.b64decode(flag64))

#'CCTF{EnCrYp7I0n_4nD_5u8STitUtIn9_iN_Fi3Ld!}'

Keybase

POINTS：48

考点：AES-CBC模式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#!/usr/bin/env python3

from Crypto.Util import number
from Crypto.Cipher import AES
import os, sys, random
from flag import flag

def keygen():
    iv, key = [os.urandom(16) for _ in '01']
    return iv, key

def encrypt(msg, iv, key):
    aes = AES.new(key, AES.MODE_CBC, iv)
    return aes.encrypt(msg)

def decrypt(enc, iv, key):
    aes = AES.new(key, AES.MODE_CBC, iv)
    return aes.decrypt(enc)

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, " hi all, welcome to the simple KEYBASE cryptography task, try to    ", border)
    pr(border, " decrypt the encrypted message and get the flag as a nice prize!    ", border)
    pr(border*72)

    iv, key = keygen()
    flag_enc = encrypt(flag, iv, key).hex()

    while True:
        pr("| Options: \n|\t[G]et the encrypted flag \n|\t[T]est the encryption \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'g':
            pr("| encrypt(flag) =", flag_enc)
        elif ans == 't':
            pr("| Please send your 32 bytes message to encrypt: ")
            msg_inp = sc()
            if len(msg_inp) == 32:
                enc = encrypt(msg_inp, iv, key).hex()
                r = random.randint(0, 4)
                s = 4 - r
                mask_key = key[:-2].hex() + '*' * 4
                mask_enc = enc[:r] + '*' * 28 + enc[32-s:]
                pr("| enc =", mask_enc)
                pr("| key =", mask_key)
            else:
                die("| SEND 32 BYTES MESSAGE :X")
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

是一道需要交互的题目，那么我们看到题目提供的功能。

一个是 g，会将flag的密文输出

1
2
if ans == 'g':
	pr("| encrypt(flag) =", flag_enc)

一个是 t，接受32字节的消息加密，然后输出密钥前14字节，以及相应密文，不过会对密文第一组做一个隐藏处理，只给出第一组开头和结尾共4个字节

1
2
3
4
5
6
7
8
9
10
11
elif ans == 't':
    pr("| Please send your 32 bytes message to encrypt: ")
    msg_inp = sc()
    if len(msg_inp) == 32:
        enc = encrypt(msg_inp, iv, key).hex()
        r = random.randint(0, 4)
        s = 4 - r
        mask_key = key[:-2].hex() + '*' * 4
        mask_enc = enc[:r] + '*' * 28 + enc[32-s:]
        pr("| enc =", mask_enc)
        pr("| key =", mask_key)

而加密和解密使用的是AES-CBC模式

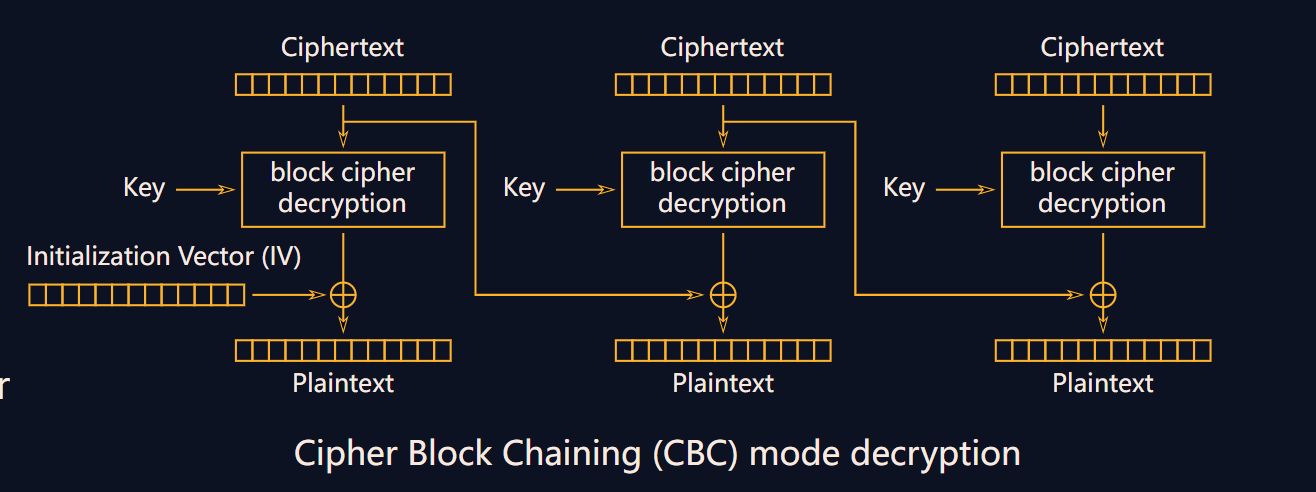
image-20220712140756535

所以这里的切入点很明确，就是利用功能 t，

  1. 首先我们发送两组共32字节的明文 “A”*32 过去，会得到14字节的密钥和一组模糊密文和一组清晰密文
  2. 我们爆破密钥的剩余两个字节，然后用爆破出来的密钥尝试对第二组密文进行解密，解密后的结果和第一组模糊密文中的清晰部分进行异或，如果得到的均为”A“，则我们的密钥爆破正确。
  3. 由于CBC模式，我们还需要iv。此时我们拥有密钥，明文；如果拥有第一组密文，我们对第一组密文进行解密并与明文异或即可知道iv
  4. 需要意识到的是，第一组密文用于第二组明文加密，而第二组明文我们又是知道的，所以我们使用密钥解密第二组密文，并与第二组明文异或得到第一组密文，然后解密第一组密文，与第一组明文异或，得到iv
  5. 使用密钥和iv解密flag的密文，获取flag

脚本改编自https://blog.cryptohack.org/cryptoctf2021-easy#keybase

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from pwn import *
from Crypto.Cipher import AES


context.log_level = 'debug'
r = process(["python3","keybase.py"])


r.sendlineafter("[Q]uit\n", "G")
enc_flag = bytes.fromhex(r.recvline().strip().decode().split(" = ")[1])


while True:
    r.sendlineafter("[Q]uit\n", "T")
    r.sendlineafter("Please send your 32 bytes message to encrypt: \n", b"A"*32)
    enc = r.recvline().strip().decode().split(" = ")[1]
    key = r.recvline().strip().decode().split(" = ")[1]
    prefix = enc.split("*")[0]
    if len(prefix) == 4:
        prefix = bytes.fromhex(prefix)
        break

key = bytearray.fromhex(key[:-4]) + b"\x00\x00"
for k1 in range(256):
    key[-2] = k1
    for k2 in range(256):
        key[-1] = k2
        if xor(AES.new(key, AES.MODE_ECB).decrypt(bytes.fromhex(enc[-32:])), b"AA")[:2] == prefix:
            block = xor(AES.new(key, AES.MODE_ECB).decrypt(bytes.fromhex(enc[-32:])), b"A"*16)
            IV = xor(AES.new(key, AES.MODE_ECB).decrypt(block)[:16], b"A"*16)
            print("key",key.hex())
            print("IV",IV.hex())
            print(AES.new(key, AES.MODE_CBC, IV).decrypt(enc_flag))
            exit()

Rima

POINTS:56

考点：爆破，信息恢复

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#!/usr/bin/env python

from Crypto.Util.number import *
#from flag import FLAG
from sympy import isprime
FLAG=b'CCTF{_how_finD_7h1s_1z_s3cr3T?!}'
def nextPrime(n):
    while True:
        n += (n % 2) + 1
        if isprime(n):
            return n

f = [int(x) for x in bin(int(FLAG.hex(), 16))[2:]]

print(len(f))
f.insert(0, 0)
for i in range(len(f)-1):
    f[i] += f[i+1]
a = nextPrime(len(f))
b = nextPrime(a)
print(a,b)
g, h = [[_ for i in range(x) for _ in f] for x in [a, b]]
print(len(g),len(h))
print('-'*100)

print(len(g),len(h))
c = nextPrime(len(f) >> 2)
print(c)
for _ in [g, h]:
    for __ in range(c):
        _.insert(0, 0)

    for i in range(len(_) -  c):
        _[i] += _[i+c]

g, h = [int(''.join([str(_) for _ in __]), 5) for __ in [g, h]]

# for _ in [g, h]:
#     if _ == g:
#         fname = 'g'
#     else:
#         fname = 'h'
#     of = open(f'{fname}.enc', 'wb')
#     of.write(long_to_bytes(_))
#     of.close()

这道题的函数很简单，一个nextPrime，顾名思义。

然后程序对flag取二进制，然后在最开始插入一个0。如果flag是这个比赛的常规flag，那么会以‘C’开头，而‘C’的ASCII码的二进制是“01‘开头，所以补上这个0后，不出意外这个f数组的长度应该是8 * len(flag)。

1
2
3
4
f = [int(x) for x in bin(int(FLAG.hex(), 16))[2:]]

print(len(f))
f.insert(0, 0)

然后进行一个操作，f数组的每一个（除了最后一个）元素赋值为当前元素和后一个元素值之和。

1
2
for i in range(len(f)-1):
    f[i] += f[i+1]

然后程序获取三个值 a = nextPrime(len(f)), b = nextPrime(a), c = nextPrime(len(f) >> 2)。三个值的取值只与flag的长度相关。（那么显然最后可以通过爆破flag的长度来解题）

1
2
a = nextPrime(len(f))
b = nextPrime(a)

然后是有点绕的一个数组生成 ，其实就是将数组f 分别重复 a次 和 b次。

1
g, h = [[_ for i in range(x) for _ in f] for x in [a, b]]

接着给g，h前面插c个0，

然后与之前类似的一个操作，g和h数组的每一个（除了后面c个）元素赋值为当前元素和后C个元素值之后。

1
2
3
4
5
6
for _ in [g, h]:
    for __ in range(c):
        _.insert(0, 0)

    for i in range(len(_) -  c):
        _[i] += _[i+c]

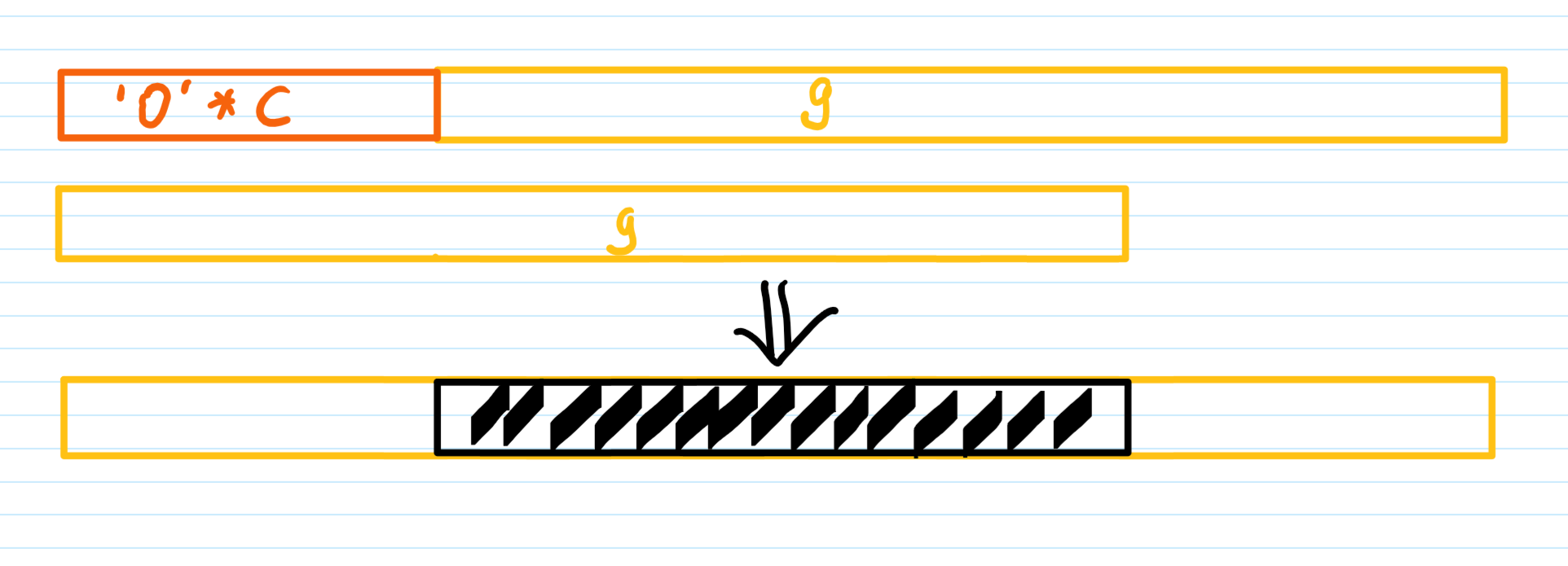image-20210804173731885类似这样两个数组相加。最后还将当前得到的值拼接，视为五进制

1
g, h = [int(''.join([str(_) for _ in __]), 5) for __ in [g, h]]

所以解题思路就很清晰。

  1. 首先我们爆破flag的长度，我们知道密文的长度为 a * f + c 和 b * f + c，而a ,b,c 又和f直接相关，所以这很好判断。

  2. 然后我们先恢复这个”移位C“的向量加，以上图为例，由于最后结果仍然保留了原来g数组的开头和结尾，故中间部分是很好恢复的。

  3. 最后我们在恢复一个”移位1“的向量加即可解出flag。

（其实用不到两个enc，有一个就够了。）

exp.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from Crypto.Util.number import *

def to_base_5(n):
    s = ''
    while n:
        s = str(n % 5) + s
        n //= 5
    return s

def nextPrime(n):
    while True:
        n += (n % 2) + 1
        if isPrime(n):
            return n

with open('g.enc', 'rb') as f:
    data = f.read()
    g_long = bytes_to_long(data)

g_base5 = to_base_5(g_long)
g = [x for x in g_base5]

for len in range(55):
    f = len * 8
    a = nextPrime(f)
    b = nextPrime(a)
    c = nextPrime(f >> 2)
    
    if len(g) != a * f + c:
        continue

    g = [int(x) for x in g]

    for i in range(len(g) - c - 1, -1, -1):
        g[i] -= g[i+c]

    g = g[c:c+f]
    
    for i in range(len(g) - 1 - 1, -1, -1):
        g[i] -= g[i+1]
        
    g = [str(x) for x in g]
    g = int(''.join(g), 2)
    g = long_to_bytes(g) 
    print(g)
    
    #CCTF{_how_finD_7h1s_1z_s3cr3T?!}

Titu

POINTS：69

考点：丢番图方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

l = len(flag)
m_1, m_2 = flag[: l // 2], flag[l // 2:]

x, y = bytes_to_long(m_1), bytes_to_long(m_2)

k = '''
000bfdc32162934ad6a054b4b3db8578674e27a165113f8ed018cbe9112
4fbd63144ab6923d107eee2bc0712fcbdb50d96fdf04dd1ba1b69cb1efe
71af7ca08ddc7cc2d3dfb9080ae56861d952e8d5ec0ba0d3dfdf2d12764
'''.replace('\n', '')

assert((x**2 + 1)*(y**2 + 1) - 2*(x - y)*(x*y - 1) == 4*(int(k, 16) + x*y))

代码倒是不多，眼瞅着就是一道数学题

解方程 $(x^2+1)\cdot(y^2+1)-2\cdot(x-y)(xy-1) == 4\cdot(k+xy)$

用sage整理一下

1
2
3
4
5
sage: var('x,y')
(x, y)
sage: f = (x**2 + 1)*(y**2 + 1) - 2*(x - y)*(x*y - 1) - 4*x*y
sage: f.factor()
(x + 1)^2*(y - 1)^2

$(x^2+1)\cdot(y^2+1)-2\cdot(x-y)(xy-1) - 4xy = ((x+1)(y+1))^2$

那看看这个 k 是不是平方数

1
2
3
4
sage: k
246389259423689900229483388850933720271363907782961941639413620688310657308991195363798484778005049234253341752674411282663124201840620584781830032437353134292733496201534415265400175632719346764031781179041636
sage: factor(k)
2^2 * 3^2 * 11^4 * 19^2 * 47^2 * 71^2 * 3449^2 * 11953^2 * 5485619^2 * 2035395403834744453^2 * 17258104558019725087^2 * 1357459302115148222329561139218955500171643099^2

$k=(2\cdot 3\cdot 11^2\cdot 19\cdot 47\cdot 71\cdot 3449\cdot 11953\cdot 5485619\cdot 2035395403834744453 \cdot 17258104558019725087 \cdot 1357459302115148222329561139218955500171643099)^2$

那开个方的话，就是解 $(x+1)(y+1)=2^2\cdot 3\cdot 11^2\cdot 19\cdot 47\cdot 71\cdot 3449\cdot 11953\cdot 5485619\cdot 2035395403834744453 \cdot 17258104558019725087 \cdot 1357459302115148222329561139218955500171643099$

然后这里 x 和 y 的长度大小应该是比较接近的，emmm，排列组合一下？方程右边的分一分，给到 (x+1) 和 (y+1)

或者换个意思，显然 $(x+1) \mid 2\sqrt{k}$，遍历一下 $2\sqrt{k}$ 的因子那就

脚本来自https://blog.cryptohack.org/cryptoctf2021-easy#titu

1
2
3
4
5
6
7
8
9
10
11
12
from Crypto.Util.number import *
from gmpy2 import iroot
k = 246389259423689900229483388850933720271363907782961941639413620688310657308991195363798484778005049234253341752674411282663124201840620584781830032437353134292733496201534415265400175632719346764031781179041636 
m = iroot(k,int(2))[0] * 2
 
for d in divisors(m):   
    x = long_to_bytes(d - 1)   
    if b'CCTF{' in x:  
        print(x)  
        y = (m // d) + 1 
        print(long_to_bytes(y))
        break

Symbols

POINTS：70

考点：latex

h, my eyes, my eyes! People still can solve this kind of cryptography? Mathematicians should love this one! 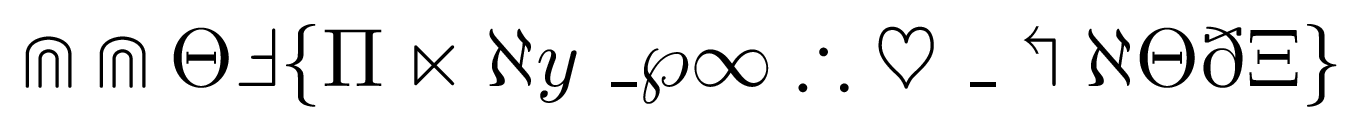Symbols Challenge

1
\Cap \Cap \Theta \Finv \{ \Pi \ltimes \aleph y \_ \wp \infty \therefore \heartsuit \_ \Lsh \aleph \Theta \eth \Xi \}

$\Cap \Cap \Theta \Finv { \Pi \ltimes \aleph y _ \wp \infty \therefore \heartsuit _ \Lsh \aleph \Theta \eth \Xi }$

CCTF{Play_with_LaTeX}

Hyper Normal

POINTS：71

考点：Matrix，爆破

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import random
from flag import FLAG

p = 8443

def transpose(x):
    result = [[x[j][i] for j in range(len(x))] for i in range(len(x[0]))]
    return result

def vsum(u, v):
    assert len(u) == len(v)
    l, w = len(u), []
    for i in range(l):
        w += [(u[i] + v[i]) % p]
    return w

def sprod(a, u):
    w = []
    for i in range(len(u)):
        w += [a*u[i] % p]
    return w

def encrypt(msg):
    l = len(msg)
    hyper = [ord(m)*(i+1) for (m, i) in zip(list(msg), range(l))]
    V, W = [], []
    for i in range(l):
        v = [0]*i + [hyper[i]] + [0]*(l - i - 1)
        V.append(v)
    random.shuffle(V)
    for _ in range(l):
        R, v = [random.randint(0, 126) for _ in range(l)], [0]*l
        for j in range(l):
            v = vsum(v, sprod(R[j], V[j]))  
        W.append(v)
    
    random.shuffle(transpose(W))
    return W

enc = encrypt(FLAG)
print(enc)

output =

分析上述源码，可以知道，

transpose函数为矩阵转置

1
2
3
def transpose(x):
    result = [[x[j][i] for j in range(len(x))] for i in range(len(x[0]))]
    return result

vsum函数为向量加法

1
2
3
4
5
6
def vsum(u, v):
    assert len(u) == len(v)
    l, w = len(u), []
    for i in range(l):
        w += [(u[i] + v[i]) % p]
    return w

sprod函数为向量的倍增

1
2
3
4
5
def sprod(a, u):
    w = []
    for i in range(len(u)):
        w += [a*u[i] % p]
    return w

看到加密函数encrypt

首先生成hyper向量，向量的每个值与flag每个字节相关，为 $ord(flag_i) \cdot (i+1), i \in [0,len(flag)]$，

然后用hyper向量生成对角矩阵V，效果为$[a,b,c,d,e] \rightarrow$ $$\begin{bmatrix}a&0&0&0&0\newline 0&b&0&0&0\newline 0&0&c&0&0\newline 0&0&0&d&0\newline 0&0&0&0&e\newline\end{bmatrix}$$

然后利用shuffle函数扰乱一下行向量。

1
2
3
4
5
6
7
8
def encrypt(msg):
    l = len(msg)
    hyper = [ord(m)*(i+1) for (m, i) in zip(list(msg), range(l))]
    V, W = [], []
    for i in range(l):
        v = [0]*i + [hyper[i]] + [0]*(l - i - 1)
        V.append(v)
    random.shuffle(V)

之后生成 l 个 R向量，用于生成w矩阵，规则为v = vsum(v, sprod(R[j], V[j])) 

1
2
3
4
5
for _ in range(l):
    R, v = [random.randint(0, 126) for _ in range(l)], [0]*l
    for j in range(l):
        v = vsum(v, sprod(R[j], V[j]))  
    W.append(v)

可以知道，这样乘了之后，之前对于V的shuffle对于结果来说其实是没有意义。由于我们并不关心 R 的实际顺序，于是等价生成了R矩阵$$\begin{bmatrix}R_{00}&R_{01}&R_{02}&R_{03}&R_{04}\newline R_{10}&R_{11}&R_{12}&R_{13}&R_{14}\newline R_{20}&R_{21}&R_{22}&R_{23}&R_{24}\newline R_{30}&R_{31}&R_{32}&R_{33}&R_{34}\newline R_{40}&R_{41}&R_{42}&R_{43}&R_{44}\newline \end{bmatrix}$$，然后和矩阵$$V=\begin{bmatrix}a&0&0&0&0\newline 0&b&0&0&0\newline 0&0&c&0&0\newline 0&0&0&d&0\newline 0&0&0&0&e\newline\end{bmatrix}$$相乘。

然后这里还有一个random.shuffle(transpose(W))函数，但是这里 shuffle 的其实是矩阵transpose(W)，而函数返回的是W矩阵，所以这句代码对返回结果其实没有任何影响。

那么我们得到矩阵 $$M = \begin{bmatrix}a \cdot R_{00} &b \cdot R_{01} &c \cdot R_{02}&d \cdot R_{03}&e \cdot R_{04}\newline a \cdot R_{10} &b \cdot R_{11}&c \cdot R_{12}&d \cdot R_{13}&e \cdot R_{14}\newline a \cdot R_{20}&b \cdot R_{21}&c \cdot R_{22}&d \cdot R_{23}&e \cdot R_{24}\newline a \cdot R_{30}&b \cdot R_{31}&c \cdot R_{32}&d \cdot R_{33}&e \cdot R_{34}\newline a \cdot R_{40}&b \cdot R_{41}&c \cdot R_{42}&d \cdot R_{43}&e \cdot R_{44}\newline \end{bmatrix}$$

而加密函数中两次shuffle都没了任何影响。

如果此时不是由于模运算的存在且p = 8443 太小了。那么我们对矩阵列向量求一个gcd就能过获取flag的每一个字节的值了。

所以这里的另辟蹊径。由于模运算的存在显然是逆不回去了，我们选择正向爆破。

由于这里的$R_{ij} \in(0,126)$，那么我们就尝试所有的 $R$ 和每一个可见字符

1
2
for c in printable:
    possibilities = [ord(c)*r*(idx+1) % p for r in range(127)]

如果flag密文向量中的每一个值都存在于 possibilities 向量中，那么则说明我们对于该密文向量我们的明文字符选取正确。

脚本来自 https://blog.cryptohack.org/cryptoctf2021-easy#hyper-normal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from string import printable

p = 8443

with open('output.txt', 'r') as f:
    enc = eval(f.read())

results = []

for i in range(len(enc[0])):
    tmp = []
    for j in enc:
        tmp.append(j[i])
    results.append(tmp)

flag = ''
for idx, result in enumerate(results):
    for c in printable:
        possibilities = [ord(c)*r*(idx+1) % p for r in range(127)]
        if all([i in possibilities for i in result]):
            flag += c
            break
print(flag)

Salt and Pepper

POINTS：71

考点：哈希拓展攻击

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#!/usr/bin/env python3

from hashlib import md5, sha1
import sys
from secret import salt, pepper
from flag import flag


assert len(salt) == len(pepper) == 19
assert md5(salt).hexdigest()    == '5f72c4360a2287bc269e0ccba6fc24ba'
assert sha1(pepper).hexdigest() == '3e0d000a4b0bd712999d730bc331f400221008e0'


def auth_check(salt, pepper, username, password, h):
    return sha1(pepper + password + md5(salt + username).hexdigest().encode('utf-8')).hexdigest() == h

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  welcome to hash killers battle, your mission is to login into the ", border)
    pr(border, "  ultra secure authentication server with provided information!!    ", border)
    pr(border*72)

    USERNAME = b'n3T4Dm1n'
    PASSWORD = b'P4s5W0rd'

    while True:
        pr("| Options: \n|\t[L]ogin to server \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'l':
            pr('| send your username, password as hex string separated with comma: ')
            inp = sc()
            try:
                inp_username, inp_password = [bytes.fromhex(s) for s in inp.split(',')]
            except:
                die('| your input is not valid, bye!!')
            pr('| send your authentication hash: ')
            inp_hash = sc()
            if USERNAME in inp_username and PASSWORD in inp_password:
                if auth_check(salt, pepper, inp_username, inp_password, inp_hash):
                    die(f'| Congrats, you are master in hash killing, and it is the flag: {flag}')
                else:
                    die('| your credential is not valid, Bye!!!')
            else:
                die('| Kidding me?! Bye!!!')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

看到获取flag的条件

1
2
3
if USERNAME in inp_username and PASSWORD in inp_password:
    if auth_check(salt, pepper, inp_username, inp_password, inp_hash):
        die(f'| Congrats, you are master in hash killing, and it is the flag: {flag}')

USERNAME 要在 inp_username 中，PASSWORD 要在 inp_password 中

然后满足

1
sha1(pepper + password + md5(salt + username).hexdigest().encode('utf-8')).hexdigest() == h

其中 salt，pepper 未知，但是知道 md5(salt) 和 sha1(pepper)以及salt 和 pepper 的长度；inp_username，inp_password，inp_hash可控。那么显然这里是一个哈希长度拓展攻击了。

  1. 我们知道salt的长度以及哈希，那么我们可以使用哈希拓展攻击，附加上username 并获取到 md5(salt + username) 的哈希。

    ./hash_extender -f md5 -d -s 5f72c4360a2287bc269e0ccba6fc24ba -a n3T4Dm1n -l 19

    得到

    1
    2
    95623660d3d04c7680a52679e35f041c
    \x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98\x00\x00\x00\x00\x00\x00\x00n3T4Dm1n

  2. 然后我们知道 pepper 的长度以及哈希，还知道 password，我们再次使用哈希拓展攻击，附加上 password+md5(salt + username) 的哈希并获取到最终的哈希

    1
    ./hash_extender -f sha1 -d  -s  3e0d000a4b0bd712999d730bc331f400221008e0 -a P4s5W0rd95623660d3d04c7680a52679e35f041c -l 19

    得到

    1
    2
    83875efbe020ced3e2c5ecc908edc98481eba47f
    \x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98P4s5W0rd95623660d3d04c7680a52679e35f041c

  3. 那么我们以

    用户名：\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98\x00\x00\x00\x00\x00\x00\x00n3T4Dm1n

    密码：\x80\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x98P4s5W0rd

    哈希：

    83875efbe020ced3e2c5ecc908edc98481eba47f

    作为输入即可通过验证，获取flag

工具hash_extender来自github：https://github.com/iagox86/hash_extender

下述脚本来自：https://pwnthenope.pythonanywhere.com/writeups/salt_and_pepper.html

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from pwn import remote, process
import subprocess
import re

def main():
    local = False
    username = 'n3T4Dm1n'
    password = 'P4s5W0rd'
    if local:
        md5_salt = '7ae4d6728e33ff002bf67a2e5194ccb1'
        sha1_pepper = '8923ecf3550e9ca6cbb26066590fb619a2d65e71'
    else:
        md5_salt = '5f72c4360a2287bc269e0ccba6fc24ba'
        sha1_pepper = '3e0d000a4b0bd712999d730bc331f400221008e0'

    result = subprocess.check_output(["./hash_extender", "-f", "md5", "-d", "", "-s", md5_salt, "-a", username, "-l", "19"]).decode()
    new_signature, new_username = re.findall(r"[a-fA-F0-9]{4,}", result) # hex-encoded
    
    result = subprocess.check_output(["./hash_extender", "-f", "sha1", "-d", "", "-s", sha1_pepper, "-a", password + new_signature, "-l", "19"]).decode()
    final_signature, new_password = re.findall(r"[a-fA-F0-9]{4,}", result) # hex-encoded
    
    new_password = new_password[:-64]

    print("intermediate signature =", new_signature)
    print("final signature =", final_signature)
    print("username =", new_username)
    print("password =", new_password)

    if local:
        r = process(["python", "salt_pepper.py"])
    else:
        r = remote("02.cr.yp.toc.tf", 28010)
    r.recvuntil(b'uit')
    r.recvline()
    r.sendline(b'L')
    r.recvuntil(b'comma:')
    r.recvline()
    r.sendline(",".join([new_username, new_password]).encode())
    r.recvuntil(b'hash:')
    r.recvline()
    r.sendline(final_signature.encode())
    r.interactive()

if __name__ == "__main__":
    main()

Hamul

POINTS：83

考点：RSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Crypto.Util.number import *
from flag import flag

nbit = 64

while True:
    p, q = getPrime(nbit), getPrime(nbit)
    P = int(str(p) + str(q))
    Q = int(str(q) + str(p))
    PP = int(str(P) + str(Q))
    QQ = int(str(Q) + str(P))
    if isPrime(PP) and isPrime(QQ):
        break

n = PP * QQ
m = bytes_to_long(flag.encode('utf-8'))
if m < n:
    c = pow(m, 65537, n)
    print('n =', n)
    print('c =', c)

# n = 98027132963374134222724984677805364225505454302688777506193468362969111927940238887522916586024601699661401871147674624868439577416387122924526713690754043
# c = 42066148309824022259115963832631631482979698275547113127526245628391950322648581438233116362337008919903556068981108710136599590349195987128718867420453399

emmm，RSA经典整活，就是分解特殊构造的n。

我们设 $x=len(q),y=len(p),x’=len(Q),y’=len(P)$）

那么有

$PP = P \cdot 10^{x’} + Q = (p\cdot 10^{x} +q)\cdot 10^{x’} + (q\cdot 10^{y} +p)=p\cdot (10^{x+x’})+q\cdot (10^{x’}+10^{y})+p$

$QQ = Q \cdot 10^{y’} + P = (q\cdot 10^{y} +p)\cdot 10^{y’} + (p\cdot 10^{x} +q) =q \cdot(10^{y+y’}) + p \cdot(10^y+10^{y’})+q$

$N = PP \cdot QQ = pq\cdot10^{x+x’+y+y’} + \cdots+p\cdot q$

只要我们能够解出 $pq$，因为他只有 128bit，能够大力分解，然后我们就可以解题了。

看着这里 N 的形式，本地测一下，会发现 N 的最高十八位就是 $pq$ 的高位，N 的最低十八、十九位就是 $pq$ 的低位。然后中间会缺一到两位，要爆破一下。

脚本来自https://blog.cryptohack.org/cryptoctf2021-easy#hamul

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
from tqdm import tqdm

n = 98027132963374134222724984677805364225505454302688777506193468362969111927940238887522916586024601699661401871147674624868439577416387122924526713690754043
c = 42066148309824022259115963832631631482979698275547113127526245628391950322648581438233116362337008919903556068981108710136599590349195987128718867420453399

low = str(n)[-18:]
high = str(n)[:18]
pq_prob = []

for i in range(10):
    for j in range(10):
        pq_prob.append(int(high + str(i) + str(j)+ low))
        
for x in tqdm(pq_prob):
    f = factor(x)
    if (len(f) == 2 and f[0][0].nbits() == 64):
        p, q = f[0][0], f[1][0]
        break

P = int(str(p) + str(q))
Q = int(str(q) + str(p))
PP = int(str(P) + str(Q))
QQ = int(str(Q) + str(P))
N = PP * QQ
assert N == n
phi = (PP-1) * (QQ-1)
d = inverse(e, phi)
m = pow(c, d, p*q)
print(long_to_bytes(m))

Triplet

POINTS：91

考点：RSA，欧拉函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#!/usr/bin/env python3

from Crypto.Util.number import *
from random import randint
import sys
flag='a'*55

def die(*args):
	pr(*args)
	quit()

def pr(*args):
	s = " ".join(map(str, args))
	sys.stdout.write(s + "\n")
	sys.stdout.flush()

def sc():
	return sys.stdin.readline().strip()

def main():
	border = "+"
	pr(border*72)
	pr(border, " hi talented cryptographers, the mission is to find the three RSA   ", border)
	pr(border, " modulus with the same public and private exponent! Try your chance!", border)
	pr(border*72)

	nbit = 160

	while True:
		pr("| Options: \n|\t[S]end the three nbit prime pairs \n|\t[Q]uit")
		ans = sc().lower()
		order = ['first', 'second', 'third']
		if ans == 's':
			P, N = [], []
			for i in range(3):
				pr("| Send the " + order[i] + " RSA primes such that nbit >= " + str(nbit) + ": p_" + str(i+1) + ", q_" + str(i+1) + " ")
				params = sc()
				try:
					p, q = params.split(',')
					p, q = int(p), int(q)
				except:
					die("| your primes are not valid!!")
				if isPrime(p) and isPrime(q) and len(bin(p)[2:]) >= nbit and len(bin(q)[2:]) >= nbit:
					P.append((p, q))
					n = p * q
					N.append(n)
				else:
					die("| your input is not desired prime, Bye!")
			if len(set(N)) == 3:
				pr("| Send the public and private exponent: e, d ")
				params = sc()
				try:
					e, d = params.split(',')
					e, d = int(e), int(d)
				except:
					die("| your parameters are not valid!! Bye!!!")
				phi_1 = (P[0][0] - 1)*(P[0][1] - 1)
				phi_2 = (P[1][0] - 1)*(P[1][1] - 1)
				phi_3 = (P[2][0] - 1)*(P[2][1] - 1)
				if 1 < e < min([phi_1, phi_2, phi_3]) and 1 < d < min([phi_1, phi_2, phi_3]):
					b = (e * d % phi_1 == 1) and (e * d % phi_2 == 1) and (e * d % phi_3 == 1)
					if b:
						die("| You got the flag:", FLAG)
					else:
						die("| invalid exponents, bye!!!")
				else:
					die("| the exponents are too small or too large!")
			else:
				die("| kidding me?!!, bye!")
		elif ans == 'q':
			die("Quitting ...")
		else:
			die("Bye ...")

if __name__ == '__main__':
	main()

可以看到题目逻辑很简单，就是让你输入三对 p,q，在同一对 e,d的情况下，均满足 $e \cdot d \equiv 1 \pmod {(p-1) \cdot (q-1)}$

1
2
if 1 < e < min([phi_1, phi_2, phi_3]) and 1 < d < min([phi_1, phi_2, phi_3]):
	b = (e * d % phi_1 == 1) and (e * d % phi_2 == 1) and (e * d % phi_3 == 1)

满足 $e \cdot d \equiv 1 \pmod {(p-1) \cdot (q-1)}$，显然会满足 $e \cdot d \equiv 1 \pmod {LCM((p-1) \cdot (q-1))}$

那么很直观的，我们想要找到一个素数 $p_0$，满足 $p_1 = \frac{p_0-1}{2}+1$ 也是一个素数，这样$(p_1-1)\cdot(q-1) = \frac{(p_0-1)}{2}\cdot(q-1)$，就能够满足条件。

同理可以再找一个$p_2 = \frac{p_0-1}{4}+1$

最后找一个合适的公钥e，1 < e < min([phi_1, phi_2, phi_3])，然后生成私钥 d = inverse(e，min([phi_1, phi_2, phi_3]))，就能够通过验证，获取flag。

何为合适？能过所有的assert的呗。(因为这里要求d = inverse(e，min([phi_1, phi_2, phi_3]))，所以会满足 $e \cdot d \equiv 1 \pmod{(p-1)\cdot(q-1)}$ ，但不一定满足$e \cdot d \equiv 1 \pmod{2\cdot (p-1)\cdot(q-1)}$

exp.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from Crypto.Util.number import *
from gmpy2 import is_prime
from tqdm import tqdm
# for _ in tqdm(range(1000)):
#     FLAG=0
#     p = getPrime(170)

#     if is_prime(2*p-1):
#         FLAG+=1
#     if is_prime(4*p-3):
#         FLAG+=1

#     if FLAG >= 2:
#         print(p,2*p-1,4*p-3)
#         break

 #46%|████████████████████████████████████▋                                          | 464/1000 [00:06<00:06, 79.88it/s]1449368757550124595394471100025923300308378816147831 2898737515100249190788942200051846600616757632295661 5797475030200498381577884400103693201233515264591321


q = getPrime(160)
p0 = 1449368757550124595394471100025923300308378816147831
p1 = 2898737515100249190788942200051846600616757632295661
p2 = 5797475030200498381577884400103693201233515264591321

phi1 = (q-1)*(p0-1)
phi2 = (q-1)*(p1-1)
phi3 = (q-1)*(p2-1)
while True:
    e = getPrime(160)
    d = inverse(e,min(phi1,phi2,phi3))
    if e*d % phi1 == 1 and e*d % phi2 == 1 and e*d % phi3 == 1 and 1 < e < min(phi1,phi2,phi3) and 1 < d < min(phi1,phi2,phi3):
        print(e,d)
        break

    
#CCTF{7HrE3_b4Bie5_c4rRi3d_dUr1nG_0Ne_pr39naNcY_Ar3_triplets}

Onlude

POINTS：95

考点：线性代数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#!/usr/bin/env sage

from sage.all import *
from flag import flag

global p, alphabet
p = 71
alphabet = '=0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ$!?_{}<>'

flag = flag.lstrip('CCTF{').rstrip('}')
assert len(flag) == 24

def cross(m):
    return alphabet.index(m)

def prepare(msg):
    A = zero_matrix(GF(p), 11, 11)
    for k in range(len(msg)):
        i, j = 5*k // 11, 5*k % 11
        A[i, j] = cross(msg[k])
    return A

def keygen():
    R = random_matrix(GF(p), 11, 11)
    while True:
        S = random_matrix(GF(p), 11, 11)
        if S.rank() == 11:
            _, L, U = S.LU()
            return R, L, U

def encrypt(A, key):
    R, L, U = key
    S = L * U
    X = A + R
    Y = S * X
    E = L.inverse() * Y
    return E

A = prepare(flag)
key = keygen()
R, L, U = key
S = L * U
E = encrypt(A, key)
print(f'E = \n{E}')
print(f'L * U * L = \n{L * U * L}')
print(f'L^(-1) * S^2 * L = \n{L.inverse() * S**2 * L}')
print(f'R^(-1) * S^8 = \n{R.inverse() * S**8}')
E = 
[25 55 61 28 11 46 19 50 37  5 21]
[20 57 39  9 25 37 63 31 70 15 47]
[56 31  1  1 50 67 38 14 42 46 14]
[42 54 38 22 19 55  7 18 45 53 39]
[55 26 42 15 48  6 24  4 17 60 64]
[ 1 38 50 10 19 57 26 48  6  4 14]
[13  4 38 54 23 34 54 42 15 56 29]
[26 66  8 48  6 70 44  8 67 68 65]
[56 67 49 61 18 34 53 21  7 48 32]
[15 70 10 34  1 57 70 27 12 33 46]
[25 29 20 21 30 55 63 49 11 36  7]
L * U * L = 
[50  8 21 16 13 33  2 12 35 20 14]
[36 55 36 34 27 28 23 21 62 17  8]
[56 26 49 39 43 30 35 46  0 58 43]
[11 25 25 35 29  0 22 38 53 51 58]
[34 14 69 68  5 32 27  4 27 62 15]
[46 49 36 42 26 12 28 60 54 66 23]
[69 55 30 65 56 13 14 36 26 46 48]
[25 48 16 20 34 57 64 62 61 25 62]
[68 39 11 40 25 11  7 40 24 43 65]
[54 20 40 59 52 60 37 14 32 44  4]
[45 20  7 26 45 45 50 17 41 59 50]
L^(-1) * S^2 * L = 
[34 12 70 21 36  2  2 43  7 14  2]
[ 1 54 59 12 64 35  9  7 49 11 49]
[69 14 10 19 16 27 11  9 26 10 45]
[70 17 41 13 35 58 19 29 70  5 30]
[68 69 67 37 63 69 15 64 66 28 26]
[18 29 64 38 63 67 15 27 64  6 26]
[ 0 12 40 41 48 30 46 52 39 48 58]
[22  3 28 35 55 30 15 17 22 49 55]
[50 55 55 61 45 23 24 32 10 59 69]
[27 21 68 56 67 49 64 53 42 46 14]
[42 66 16 29 42 42 23 49 43  3 23]
R^(-1) * S^8 = 
[51  9 22 61 63 14  2  4 18 18 23]
[33 53 31 31 62 21 66  7 66 68  7]
[59 19 32 21 13 34 16 43 49 25  7]
[44 37  4 29 70 50 46 39 55  4 65]
[29 63 29 43 47 28 40 33  0 62  8]
[45 62 36 68 10 66 26 48 10  6 61]
[43 30 25 18 23 38 61  0 52 46 35]
[ 3 40  6 45 20 55 35 67 25 14 63]
[15 30 61 66 25 33 14 20 60 50 50]
[29 15 53 22 55 64 69 56 44 40  8]
[28 40 69 60 28 41  9 14 29  4 29]

看看怎么处理flag的先

1
2
3
4
5
6
7
8
9
10
11
def cross(m):
    return alphabet.index(m)

def prepare(msg):
    A = zero_matrix(GF(p), 11, 11)
    for k in range(len(msg)):
        i, j = 5*k // 11, 5*k % 11
        A[i, j] = cross(msg[k])
    return A

A = prepare(flag)

建了个 $11 \times 11$ 的零矩阵，然后将 flag 的每一个字符转化为在字符集里的索引放了进去，两两间隔4个元素，类似这样

1
2
3
4
5
6
7
8
9
10
11
[11  0  0  0  0 11  0  0  0  0 11]
[ 0  0  0  0 11  0  0  0  0 11  0]
[ 0  0  0 11  0  0  0  0 11  0  0]
[ 0  0 11  0  0  0  0 11  0  0  0]
[ 0 11  0  0  0  0 11  0  0  0  0]
[11  0  0  0  0 11  0  0  0  0 11]
[ 0  0  0  0 11  0  0  0  0 11  0]
[ 0  0  0 11  0  0  0  0 11  0  0]
[ 0  0 11  0  0  0  0 11  0  0  0]
[ 0 11  0  0  0  0 11  0  0  0  0]
[11  0  0  0  0 11  0  0  0  0  0]

然后生成了一个密钥

1
2
3
4
5
6
7
8
9
def keygen():
    R = random_matrix(GF(p), 11, 11)
    while True:
        S = random_matrix(GF(p), 11, 11)
        if S.rank() == 11:
            _, L, U = S.LU()
            return R, L, U
            
key = keygen()

R 和 S 是一个随机矩阵，

L，U 分别是 S的下三角矩阵和上三角矩阵，会有 $S==L \times U$

然后就是加密

1
2
3
4
5
6
7
def encrypt(A, key):
    R, L, U = key
    S = L * U
    X = A + R
    Y = S * X
    E = L.inverse() * Y
    return E

$E = L^{-1} \times Y = L^{-1} \times S \times X $

$E = L^{-1} \times L \times U \times(A+R) $

$E = U \times A + U \times R$

然后题目提供了 $L \times U \times L,L^{-1} \times S^2 \times L,R^{-1} \times S^8$

想法就是怎么用题目提供的这几个东西把 $E$ 里的 $A$ 提出来叭

首先的一个想法是把 $R$ 搞出来，因为 $E$ 里面有 $R$，

因为我们有 $R^{-1} \times S^8$，所以我们搞到 $S^8$ 就行

$S^8 = (L \times U)^8 = (L \times U \times L \times U)^4$

因为我们有 $L \times \ U \times L$ ，所以我们搞到 $U$ 就行

注意到 $L^{-1} \times S^2 \times L = L^{-1} \times (L \times U)^2 \times L = U \times L \times U \times L$

所以我们也能搞到 $U$

然后我们就能从 $E$ 中提出 $A$ 来，从而获取flag了。

脚本来自https://blog.cryptohack.org/cryptoctf2021-medium#onlude

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
E = Matrix(GF(71),[[25,55,61,28,11,46,19,50,37,5,21],
[20,57,39,9,25,37,63,31,70,15,47],
[56,31,1,1,50,67,38,14,42,46,14],
[42,54,38,22,19,55,7,18,45,53,39],
[55,26,42,15,48,6,24,4,17,60,64],
[1,38,50,10,19,57,26,48,6,4,14],
[13,4,38,54,23,34,54,42,15,56,29],
[26,66,8,48,6,70,44,8,67,68,65],
[56,67,49,61,18,34,53,21,7,48,32],
[15,70,10,34,1,57,70,27,12,33,46],
[25,29,20,21,30,55,63,49,11,36,7]])

hint1 = Matrix(GF(71),[[50,8,21,16,13,33,2,12,35,20,14],
[36,55,36,34,27,28,23,21,62,17,8],
[56,26,49,39,43,30,35,46,0,58,43],
[11,25,25,35,29,0,22,38,53,51,58],
[34,14,69,68,5,32,27,4,27,62,15],
[46,49,36,42,26,12,28,60,54,66,23],
[69,55,30,65,56,13,14,36,26,46,48],
[25,48,16,20,34,57,64,62,61,25,62],
[68,39,11,40,25,11,7,40,24,43,65],
[54,20,40,59,52,60,37,14,32,44,4],
[45,20,7,26,45,45,50,17,41,59,50]])

hint2=Matrix(GF(71),[[34,12,70,21,36,2,2,43,7,14,2],
[1,54,59,12,64,35,9,7,49,11,49],
[69,14,10,19,16,27,11,9,26,10,45],
[70,17,41,13,35,58,19,29,70,5,30],
[68,69,67,37,63,69,15,64,66,28,26],
[18,29,64,38,63,67,15,27,64,6,26],
[0,12,40,41,48,30,46,52,39,48,58],
[22,3,28,35,55,30,15,17,22,49,55],
[50,55,55,61,45,23,24,32,10,59,69],
[27,21,68,56,67,49,64,53,42,46,14],
[42,66,16,29,42,42,23,49,43,3,23]])

hint3=Matrix(GF(71),[[51,9,22,61,63,14,2,4,18,18,23],
[33,53,31,31,62,21,66,7,66,68,7],
[59,19,32,21,13,34,16,43,49,25,7],
[44,37,4,29,70,50,46,39,55,4,65],
[29,63,29,43,47,28,40,33,0,62,8],
[45,62,36,68,10,66,26,48,10,6,61],
[43,30,25,18,23,38,61,0,52,46,35],
[3,40,6,45,20,55,35,67,25,14,63],
[15,30,61,66,25,33,14,20,60,50,50],
[29,15,53,22,55,64,69,56,44,40,8],
[28,40,69,60,28,41,9,14,29,4,29]])

U = hint2/hint1
R = (hint3/((hint1*U)^4)).inverse()
A = U.inverse()*E-R
alphabet = '=0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ$!?_{}<>'
flag = ''
for k in range(24):
    i, j = 5*k // 11, 5*k % 11
    flag+=alphabet[A[i, j]]
print('CCTF{'+flag+'}')

Maid

POINTS：119

考点：Rabin Cryptosystem

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#!/usr/bin/python3

from Crypto.Util.number import *
from gmpy2 import *
from secret import *
from flag import flag

global nbit
nbit = 1024

def keygen(nbit):
    while True:
        p, q = [getStrongPrime(nbit) for _ in '01']
        if p % 4 == q % 4 == 3:
            return (p**2)*q, p

def encrypt(m, pubkey):
    if GCD(m, pubkey) != 1 or m >= 2**(2*nbit - 2):
        return None
    return pow(m, 2, pubkey)

def flag_encrypt(flag, p, q):
    m = bytes_to_long(flag)
    assert m < p * q
    return pow(m, 65537, p * q)

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  hi all, welcome to Rooney Oracle, you can encrypt and decrypt any ", border)
    pr(border, "  message in this oracle, but the flag is still encrypted, Rooney   ", border)
    pr(border, "  asked me to find the encrypted flag, I'm trying now, please help! ", border)
    pr(border*72)

    pubkey, privkey = keygen(nbit)
    p, q = privkey, pubkey // (privkey ** 2)

    while True:
        pr("| Options: \n|\t[E]ncrypt message \n|\t[D]ecrypt ciphertext \n|\t[S]how encrypted flag \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'e':
            pr("| Send the message to encrypt: ")
            msg = sc()
            try:
                msg = int(msg)
            except:
                die("| your message is not integer!!")
            pr(f"| encrypt(msg, pubkey) = {encrypt(msg, pubkey)} ")
        elif ans == 'd':
            pr("| Send the ciphertext to decrypt: ")
            enc = sc()
            try:
                enc = int(enc)
            except:
                die("| your message is not integer!!")
            pr(f"| decrypt(enc, privkey) = {decrypt(enc, privkey)} ")
        elif ans == 's':
            pr(f'| enc = {flag_encrypt(flag, p, q)}')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

这里用的是 Rabin 密码系统，但是 $n=p^2 q$

然后题目提供三个功能，

e:使用公钥加密 $c \equiv msg^2 \pmod n$

d:使用私钥解密 未知

s:给出flag的密文 $c \equiv m^{65537} \pmod n$

$n$ 也没给，不过这好搞，用两次加密功能，然后 $gcd(m_1^2-c_1,m_2^2-c_2)$ 就好了。

问题出在源码没有给出这个rabin密码系统的解密代码，那么只能fuzz一下，看有没有机会分解出 $p,q$ 来。

一般都是会传一下特殊的值，比如1，0，-1这样去fuzz，但是由于本地没法搭环境，就没法自己搞测试样例了，还挺麻烦的。

（这里后面放出源码了，就模拟一下当时的场景好了。）

1
2
3
4
5
6
7
8
9
def decrypt(c, privkey):
    m_p = pow(c, (privkey + 1) // 4, privkey)
    i = (c - pow(m_p, 2)) // privkey
    j = i * inverse(2*m_p, privkey) % privkey
    m = m_p + j * privkey
    if 2*m < privkey**2:
        return m
    else:
        return privkey**2 - m

这里本地测试的时候，会发现有时候，解密的值再加密，并不能变回去，感觉就挺奇怪的。

然后测试会发现 $gcd(D(-1)-1,n) \neq 1$

那么就能分解n了，然后就是常规解密 RSA 的操作了。

脚本来自 https://blog.cryptohack.org/cryptoctf2021-medium#maid

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
from pwn import *
from Crypto.Util.number import *
from math import gcd
import random

r = remote('04.cr.yp.toc.tf', 38010)

def encrypt(msg):
    r.recvuntil(b"[Q]uit")
    r.sendline(b"E")
    r.recvuntil(b"encrypt: ")
    r.sendline(str(msg))
    r.recvuntil(b" = ")
    return int(r.recvline().strip())

def decrypt(msg):
    r.recvuntil(b"[Q]uit")
    r.sendline(b"D")
    r.recvuntil(b"decrypt: ")
    r.sendline(str(msg))
    r.recvuntil(b" = ")
    return int(r.recvline().strip())

def get_flag():
    r.recvuntil(b"[Q]uit")
    r.sendline(b"S")
    r.recvuntil(b" = ")
    return int(r.recvline().strip())

def recover_n():
    # Obtain kn
    m = 2**1536 - random.randint(1,2**1000)
    c = encrypt(m)
    n = m**2 - c
    # Remove all factors of two
    while n%2 == 0:
        n = n // 2
    # Compute a few more GCD to remove any other factors.
    for _ in range(10):
        m = 2**1536 - random.randint(1,2**1000)
        c = encrypt(m)
        n = gcd(n, m**2 - c)
    return n

def dec_flag(p,q):
    c = get_flag()
    d = pow(0x10001, -1, (p-1)*(q-1))
    m = pow(c,d,p*q)
    return long_to_bytes(m)

def recover_factors(n):
    X = decrypt(-1)
    p = gcd(X - 1, n)
    assert isPrime(p)
    q = n // (p*p) 
    assert isPrime(q)
    return p, q

n = recover_n()
p, q = recover_factors(n)
flag = dec_flag(p,q)
print(flag)
# CCTF{___Ra8!N_H_Cryp70_5YsT3M___}

这里我们回头看一下解密函数

$m_p \equiv c^{(p+1)/4} \pmod p$

$i=(c-m_p^2)//p$

$j \equiv \frac{i} {2 \cdot m_p} \pmod p$

$m = m_p + j \cdot p$

如果 $m \ge \frac{p^2}{2},return \ p^2 -m,$

如果 $m \lt \frac{p^2}{2},return \ m,$

最初加密的时候似乎也限制了 $m \lt 2^{2\cdot 1024 -2} = 2^{2046} \le p^2$

推导一下，如果传过去正常的明文 $m$，我们得到密文 $m^2 \pmod {p^2 q}$

（不难知道 $c \equiv m^2 \pmod p$，$c \equiv m^2 \pmod {p^2}$，$c \equiv m^2 \pmod q$ ）

$m_p \equiv (m^2)^{(p+1)/4} \equiv m^{(p+1)/2} \equiv m \cdot m^{(p-1)/2}\equiv \pm m \pmod p$

$i = (m^2 - m_p^2 ) // p = (m^2 + k_1p^2q - m^2 - k_2p)//p=k_1pq-k_2$

$j \equiv \frac{i}{2m_p} \equiv \frac{k_1pq-k_2}{2m_p} \equiv \frac{-k_2}{2m_p}\pmod p $

$m = m_p + j \cdot p = m_p + \frac{-k_2p}{2m_p} $ 这一步似乎是想得到 $m \pmod {p^2}$ ？

如果传 $-1$ 去解密就会有

$m_p \equiv (-1)^{(p+1)/4} \equiv 1 \ or -1\pmod p $

如果 $m_p=1$：

$i = (-1 - 1)// p = -1$

$j \equiv -2^{-1} \pmod p$

$m = 1 +j \cdot p $

那么 $gcd(m-1,n) = gcd(j\cdot p ,p^2 q) = p$

如果 $m_p=-1$：

$i = (-1 - 1- k_1p)// p = -k_1$

$j \equiv \frac{k_1}{2}\pmod p$

$m = -1 + j \cdot p $ (然而好像触发 $m \ge \frac{p^2}{2},return \ p^2 -m,$，所以得到 $m = 1-j\cdot p +p^2 $)

那么 $gcd(m-1,n) = gcd(p^2-j\cdot p ,p^2 q) = p$

比赛的时候没有给出解密函数，，emmm，就会觉得有一点点脑洞。

Wolf

PONITS：128

考点：爆破

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#!/usr/bin/env python3

from Cryptodome.Cipher import AES
import os, time, sys, random
from flag import flag

passphrase = b'HungryTimberWolf'

def encrypt(msg, passphrase, niv):
    msg_header = 'EPOCH:' + str(int(time.time()))
    msg = msg_header + "\n" + msg + '=' * (15 - len(msg) % 16)
    aes = AES.new(passphrase, AES.MODE_GCM, nonce = niv)
    enc = aes.encrypt_and_digest(msg.encode('utf-8'))[0]
    return enc

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  hi wolf hunters, welcome to the most dangerous hunting ground!!   ", border)
    pr(border, "  decrypt the encrypted message and get the flag as a nice prize!   ", border)
    pr(border*72)

    niv = os.urandom(random.randint(1, 11))
    flag_enc = encrypt(flag, passphrase, niv)

    while True:
        pr("| Options: \n|\t[G]et the encrypted flag \n|\t[T]est the encryption \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'g':
            pr(f'| encrypt(flag) = {flag_enc.hex()}')
        elif ans == 't':
            pr("| Please send your message to encrypt: ")
            msg_inp = sc()
            enc = encrypt(msg_inp, passphrase, niv).hex()
            pr(f'| enc = {enc}')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

看到题目的附件，好像把AES-GCM加密用的key都给出来了

1
passphrase = b'HungryTimberWolf'

然后iv没给，长度也不确定，但是在1 和 11之间

1
niv = os.urandom(random.randint(1, 11))

emmm，那就暴力连接，当niv=1的时候，再爆破一下niv的值进行解密，一共也就256种可能。

期望概率大概也就是 $\frac{1}{11 \cdot 256}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from pwn import *
from Crypto.Cipher import AES
import os, time, sys, random

def dec(line):
    for iv in range(256):
        a = AES.new(b'HungryTimberWolf', AES.MODE_GCM, nonce=bytes([iv]))
        flag = a.decrypt(binascii.unhexlify(line))
        if b'CTF' in flag:
            print(flag)
            exit()
            
while True:
    sh = remote('01.cr.yp.toc.tf', 27010)
    sh.recvuntil("[Q]uit\n")
    sh.sendline('g')
    sh.recvuntil("| encrypt(flag) = ")
    enc_flag = sh.recvuntil("\n")[:-1]
    dec(enc_flag)
    sh.close()

Ferman

POINTS:134

考点：高斯整数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+  hi talented participants, welcome to the FERMAN cryptography task!  +
+  Solve the given equations and decrypt the encrypted flag! Enjoy!    +
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

| Parameters generation is a bit time consuming, so please be patient :P
| Options: 
|   [P]rint encrypted flag 
|   [R]eveal the parameters 
|   [Q]uit

P
| encrypt(flag) = 6489656589950752810044571176882070993656025408411955877914111875896024399252967804237101085443293019406006339555779534657926807551928549712558667515175079267695028070934727514846970003337126120540450206565849474378607706030211234939933160392491902242074123763448231072583065175864490510115483208842110529309232348180718641618424365058379284549574700049803925884878710773408472100779358561980206902500388524570616750475958017638946408491011264747032498524679282489181606124604218147

R
    e = 65537
    isPrime(p) = True
    isPrime(q) = True
    n = p * q
    (p - 127)**2 + (q - 184)**2 = 13809252727788824044233595548226590341967726502046327883413398709726819135921363848617960542444505497356040393690402758557636039683075007984614264314802550433942617885990971202110511768121760826488944622697964930982921462840320850014092598270493079542993367042001339267321218767132063176291998391714014192946596879176425904447127657664796094937171819714510504836456988487840790317576922986001688147359646287894578550322731904860694734616037751755921771706899493873123836562784063321
    m = bytes_to_long(flag)
    c = pow(m, e, n)

经典给出 $p,q$ 相关额外信息进行对 $n$ 的分解。

给出 $hint = (p-127)^2 + (q-184)^2$

这里经过测试发现 $hint$ 是一个七次幂，即 $hint = z ^7$

1
2
3
sage: w=13809252727788824044233595548226590341967726502046327883413398709726819135921363848617960542444505497356040393690402758557636039683075007984614264314802550433942617885990971202110511768121760826488944622697964930982921462840320850014092598270493079542993367042001339267321218767132063176291998391714014192946596879176425904447127657664796094937171819714510504836456988487840790317576922986001688147359646287894578550322731904860694734616037751755921771706899493873123836562784063321
sage: w^(1/7)
542387941227387369715206573048698209530476609597527643690717423409961

设$x=p-127,y=q-184$

那么我们有 $x^2+y^2 = z^7$

由于 $x^2+y^2 = (x+iy)(x-iy)$，

若我们能将 $z$ 分解成共轭的两部分$z_x,z_y$，那么就会有 $x+iy=z_x^7 \ or \ x+iy=z_y^7 $ 

1
2
3
sage: C = ZZ[i]
sage: factor(C(z))
(-15642728159752*I - 39850152715295) * (13420641811410*I - 19188039291907) * (19188039291907*I - 13420641811410) * (-4190*I - 9649) * (4190*I - 9649) * (-18*I - 17) * (-3*I - 8) * (3*I - 8) * (-3*I + 10) * (3*I + 10) * (17*I + 18) * (-15642728159752*I + 39850152715295)

很对称，但是emmm，排列组合太多了，，我们可以换一组数据

1
2
3
4
a = 2265 
b = 902 
w = 24007015341450638047707811509679207068051724063799752621201994109462561550079479155110637624506028551099549192036601169213196430196182069103932872524092047760624845002308713558682251660517182097667675473038586407097498167776645896369165963981698265040400341878755056463554861788991872633206414266159558715922583613630387512303492920597052611976890648632123534922756985895479931541478630417251021677032459939450624439421018438357005854556082128718286537575550378203702362524442461229
flag_enc = 10564879569008106132040759805988959471544940722100428235462653367215001622634768902220485764070394703676633460036566842009467954832811287152142597331508344786167188766356935684044757086902094847810694941751879500776345600036096556068243767090470376672110936445246103465175956767665996275085293250901512809704594905257754009538501795362031873203086994610168776981264025121998840163864902563628991590207637487738286741829585819040077197755226202284847
1
2
3
4
5
6
7
a = 2265 
b = 902 
z = w^(1/7)
C = ZZ[i]
factor(C(z))

(-I) * (-1236649975237776943493190425869173*I - 3575914522629734831030006136433790) * (-5*I - 4) * (4*I + 5) * (-1236649975237776943493190425869173*I + 3575914522629734831030006136433790)

测试

1
2
3
4
5
6
7
8
9
w = 24007015341450638047707811509679207068051724063799752621201994109462561550079479155110637624506028551099549192036601169213196430196182069103932872524092047760624845002308713558682251660517182097667675473038586407097498167776645896369165963981698265040400341878755056463554861788991872633206414266159558715922583613630387512303492920597052611976890648632123534922756985895479931541478630417251021677032459939450624439421018438357005854556082128718286537575550378203702362524442461229
zx = (-1236649975237776943493190425869173*I + 3575914522629734831030006136433790) * (-5*I - 4)
x = abs((zx^7).imag())
y = abs((zx^7).real())
print(x)
print(y)
assert x^2+y^2 == w
is_prime(x+2265)
is_prime(x+902)

返回

1
2
3
4
3515251100858858796435724523870761115321577101490666287216209907489403476079222276536571942496157069855565014771125798502774268554017196492328530962886884456876064742139864478104832820555776577341055529681241338289453827370647829795170811402
3413213301181339793171422358348736699126965473930685311400429872075816456893055375667482794611435574843396575239764759040242158681190020317082329009191911152126267671754529169503180596722173728126136891139303943035843711591741985591269095075
True
False

于是我们得到素数

1
x+2265=3515251100858858796435724523870761115321577101490666287216209907489403476079222276536571942496157069855565014771125798502774268554017196492328530962886884456876064742139864478104832820555776577341055529681241338289453827370647829795170813667
1
2
3
4
5
6
7
8
from Crypto.Util.number import *

p = 3515251100858858796435724523870761115321577101490666287216209907489403476079222276536571942496157069855565014771125798502774268554017196492328530962886884456876064742139864478104832820555776577341055529681241338289453827370647829795170813667  
q = 3413213301181339793171422358348736699126965473930685311400429872075816456893055375667482794611435574843396575239764759040242158681190020317082329009191911152126267671754529169503180596722173728126136891139303943035843711591741985591269095977
phi = (p-1)*(q-1)
d = pow(0x10001, -1, phi)
print(long_to_bytes(pow(flag_enc,d,p*q)))
b'CCTF{Congrats_Y0u_5OLv3d_x**2+y**2=z**7}'

（PS：对于方程$x^2+y^2=z^7$，我们利用高斯分解似乎能够找到很多组满足条件的解 $x,y$，取决于高斯分解 $z$ 后它能有多少个因子）

RSAphantine

POINTS:142

考点：丢番图方程

1
2
3
4
5
6
7
8
9
2*z**5 - x**3 + y*z = 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613520747411963822349374260144229698759495359592287331083229572369186844312169397998958687629858407857496154424105344376591742814310010312178029414792153520127354594349356721
x**4 + y**5 + x*y*z = 89701863794494741579279495149280970802005356650985500935516314994149482802770873012891936617235883383779949043375656934782512958529863426837860653654512392603575042842591799236152988759047643602681210429449595866940656449163014827637584123867198437888098961323599436457342203222948370386342070941174587735051
y**6 + 2*z**5 + z*y = 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613609786612391835856376321085593999733543104760294208916442207908167085574197779179315081994735796390000652436258333943257231020011932605906567086908226693333446521506911058
p = nextPrime(x**2 + z**2 + y**2 << 76)
q = nextPrime(z**2 + y**3 - y*x*z ^ 67)
n, e = p * q, 31337
m = bytes_to_long(FLAG)
c = pow(m, e, n)
c = 486675922771716096231737399040548486325658137529857293201278143425470143429646265649376948017991651364539656238516890519597468182912015548139675971112490154510727743335620826075143903361868438931223801236515950567326769413127995861265368340866053590373839051019268657129382281794222269715218496547178894867320406378387056032984394810093686367691759705672

题目的target很明显了，显然解关于x,y,z的方程组了。

  1. $2z^5 - x^3 + yz=a $

  2. $x^4+y^5+xyz=b$

  3. $y^6+2z^5+zy=c$

很直观的会想要用3式减去 1式

$y^6+x^3=c-a$

用sage处理一下

1
2
3
4
5
sage: f=y^6+x^3
sage: factor(f)
(y^4 - x*y^2 + x^2)*(y^2 + x)
sage: factor(c-a)
3133713317731333 * 28413320364759425177418147555143516002041291710972733253944530195017276664069717887927099709630886727522090965378073004342203980057853092114878433424202989

（感觉出题人处理的比较好，c-a只有两个因子）那么显然，这里有 $y^2+x=3133713317731333$

有了这一条我们再代入 $f=y^6+x^3$ 就可以解出 $x,y$ 了

有了 $x,y$ 代入 2 式就能解出 $z$ 了。

从而进行RSA参数的生成，解密获得flag。

脚本来自https://jsur.in/posts/2021-08-01-crypto-ctf-2021-writeups

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import *

c1 = 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613520747411963822349374260144229698759495359592287331083229572369186844312169397998958687629858407857496154424105344376591742814310010312178029414792153520127354594349356721
c2 = 89701863794494741579279495149280970802005356650985500935516314994149482802770873012891936617235883383779949043375656934782512958529863426837860653654512392603575042842591799236152988759047643602681210429449595866940656449163014827637584123867198437888098961323599436457342203222948370386342070941174587735051
c3 = 47769864706750161581152919266942014884728504309791272300873440765010405681123224050402253883248571746202060439521835359010439155922618613609786612391835856376321085593999733543104760294208916442207908167085574197779179315081994735796390000652436258333943257231020011932605906567086908226693333446521506911058

R.<x,y,z> = PolynomialRing(QQ)
delta = 3133713317731333
f1 = y^6 + (delta - y^2)^3 - (c3 - c1)
y = f1.univariate_polynomial().roots()[0][0]
x = delta - y^2
f2 = x^4 + y^5 + x*y*z - c2
z = f2.univariate_polynomial().roots()[0][0]

x = int(x)
y = int(y)
z = int(z)

p = Integer(x**2 + z**2 + y**2 << 76).next_prime()
q = Integer(z**2 + y**3 - y*x*z ^^ 67).next_prime()
n, e = p * q, 31337
c = 486675922771716096231737399040548486325658137529857293201278143425470143429646265649376948017991651364539656238516890519597468182912015548139675971112490154510727743335620826075143903361868438931223801236515950567326769413127995861265368340866053590373839051019268657129382281794222269715218496547178894867320406378387056032984394810093686367691759705672
d = pow(e, -1, (p-1)*(q-1))
m = pow(c, int(d), n)
print(long_to_bytes(m).decode())
CCTF{y0Ur_jO8_C4l13D_Diophantine_An4LySI5!}

FROZEN

POINTS: 142

考点：已知明文攻击（非预期？）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
from Crypto.Util.number import *
from gmpy2 import *
import sys, random, string

flag = 'fakeflag{}'

def genrandstr(N):
    return ''.join(random.choice(string.ascii_uppercase + string.digits + string.ascii_lowercase) for _ in range(N))

def paramaker(nbit):
    p = getPrime(nbit)
    r = getRandomRange(1, p)
    return p, r

def keygen(params, l, d):
    p, r = params
    s = getRandomRange(1, p)
    U = [pow(r, c + 1, p) * s % p for c in range(0,l)]
    V = [int(bin(u)[2:][:-d] + '0' * d, 2) for u in U]
    S = [int(bin(u)[2:][-d:], 2) for u in U]
    privkey, pubkey = S, V
    return pubkey, privkey

def sign(msg, privkey, d):
    msg = msg.encode('utf-8')
    l = len(msg) // 4
    M = [bytes_to_long(msg[4*i:4*(i+1)]) for i in range(l)]
    q = int(next_prime(max(M)))
    sign = [M[i]*privkey[i] % q for i in range(l)]
    return sign

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, " hi young cryptographers, welcome to the frozen signature battle!!  ", border)
    pr(border, " Your mission is to forge the signature for a given message, ready?!", border)
    pr(border*72)

    randstr = genrandstr(20)
    nbit, dbit = 128, 32
    params = paramaker(nbit)
    l = 5
    pubkey, privkey = keygen(params, l, dbit)

    while True:
        pr("| Options: \n|\t[S]how the params \n|\t[P]rint pubkey \n|\t[E]xample signature \n|\t[F]orge the signature \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 's':
            pr(f'| p = {params[0]}')
            pr(f'| r = {params[1]}')
        elif ans == 'p':
            pr(f'pubkey = {pubkey}')
        elif ans == 'e':
            pr(f'| the signature for "{randstr}" is :')
            pr(f'| signature = {sign(randstr, privkey, dbit)}')
        elif ans == 'f':
            randmsg = genrandstr(20)
            pr(f'| send the signature of the following message like example: {randmsg}')
            SIGN = sc()
            try:
                SIGN = [int(s) for s in SIGN.split(',')]
            except:
                die('| your signature is not valid! Bye!!')
            if SIGN == sign(randmsg, privkey, dbit):
                die(f'| Congrats, you got the flag: {FLAG}')
            else:
                die(f'| Your signature is not correct, try later! Bye!')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

题目是一个签名服务，使用私钥对4个字节的明文进行签名 $sign = priv_i \cdot m_p \pmod p$

$p$ 是一个约为 30bit 的素数

私钥的生成来源于 $r^is \pmod p,i \in [0,1,2,3,4]$ 的低 32 位。

但是题目给出了一个消息的签名示例，利用其 $msg,sign$，我们可以恢复 $priv_i \pmod p$

但是由于 $p$ 只有30比特左右，所以我们还需要做一点点小小的爆破，而判断依据则是 $(pub_i + pri_i) / (pub_{i-1}+pri_{i-1}) \equiv r \pmod p$

exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from Crypto.Util.number import *
from gmpy2 import *

# 交互获取签名样例计算大部分私钥: e
msg = "gxOy9KYScvLF2tWUpkg0".encode('utf-8')


l = len(msg) // 4
M = [bytes_to_long(msg[4*i:4*(i+1)]) for i in range(l)]
q = int(next_prime(max(M)))
sign = [289279587, 50849811, 1632438391, 537783778, 611375482]
privkey = [inverse(M[i],q)*sign[i] % q for i in range(l)]

# 交互获取公钥: p
pubkey = [43888590349289262389019236090217758720, 17879334018861290280325290839018307584, 40499489748639202207722187467891146752, 178025246158865738197422650069448916992, 96934554205183278449061380907857870848]

key=[]
for i in range(5):
	key.append(pubkey[i]+privkey[i])
	
# 交互获取参数: s
p = 178511102601149595520550176105220942341
r = 125432576416753760620313745406675102980

# 爆破剩余私钥
for i in range(0,4):
	for j in range(0,4):
		if (key[1]+j*q) * inverse(key[0]+i*q,p)%p == r:
			key[0] += i*q
			key[1] += j*q
			print(i,j)
			break

for i in range(2,5):
	for k in range(0,4):
		if (key[i]+k*q) * inverse(key[i-1],p)%p == r:
			key[i] += k*q
			print(i,k)
			break
privkey = [each % (2**32) for each in key]

def sign(msg, privkey):
    msg = msg.encode('utf-8')
    l = len(msg) // 4
    M = [bytes_to_long(msg[4*i:4*(i+1)]) for i in range(l)]
    q = int(next_prime(max(M)))
    sign = [M[i]*privkey[i] % q for i in range(l)]
    return sign
    
# 交互伪造签名: f
print(sign("4bV9K70jeYOoogSnGsTc", privkey))

PS：这道题的flag是 CCTF{Lattice_bA5eD_T3cHn1QuE_70_Br34K_LCG!!}，看来作者原意应该是让我们有lattice去恢复未知位，不过这里通过已知明文攻击能够获取到的低位太多了，这里需要再稍微调整一下。

LINDA

POINTS：169

考点：离散对数，$p-1$ 光滑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#!/usr/bin/env python3

from Crypto.Util.number import *
from math import gcd
from flag import flag

def keygen(p):
    while True:
        u = getRandomRange(1, p)
        if pow(u, (p-1) // 2, p) != 1:
            break
    x = getRandomRange(1, p)
    w = pow(u, x, p)
    while True:
        r = getRandomRange(1, p-1)
        if gcd(r, p-1) == 1:
            y = x * inverse(r, p-1) % (p-1)
            v = pow(u, r, p)
            return u, v, w
    
def encrypt(m, pubkey):
    p, u, v, w = pubkey
    assert m < p
    r, s = [getRandomRange(1, p) for _ in '01']
    ca = pow(u, r, p)
    cb = pow(v, s, p)
    cc = m * pow(w, r + s, p) % p
    enc = (ca, cb, cc)
    return enc

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  .:::::: LINDA Cryptosystem has high grade security level ::::::.  ", border)
    pr(border, "  Can you break this cryptosystem and find the flag?                ", border)
    pr(border*72)

    pr('| please wait, preparing the LINDA is time consuming...')
    from secret import p
    u, v, w = keygen(p)
    msg = bytes_to_long(flag)
    pubkey = p, u, v, w
    enc = encrypt(msg, pubkey)
    while True:
        pr("| Options: \n|\t[E]xpose the parameters \n|\t[T]est the encryption \n|\t[S]how the encrypted flag \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'e':
            pr(f'| p = {p}')
            pr(f'| u = {u}')
            pr(f'| v = {v}')
            pr(f'| w = {w}')
        elif ans == 's':
            print(f'enc = {enc}')
        elif ans == 't':
            pr('| send your message to encrypt: ')
            m = sc()
            m = bytes_to_long(m.encode('utf-8'))
            pr(f'| encrypt(m) = {encrypt(m, pubkey)}')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

这道题目有一个 from secret import p，交互获取样例会发现 $p-1$ 是光滑的

1
2
p = 31236959722193405152010489304408176327538432524312583937104819646529142201202386217645408893898924349364771709996106640982219903602836751314429782819699
p - 1 = 2 * 3 * 11 * 41 * 137 * 223 * 7529 * 14827 * 15121 * 40559 * 62011 * 429083 * 916169 * 3810461 * 4316867 * 20962993 * 31469027 * 81724477 * 132735437 * 268901797 * 449598857 * 2101394579 * 2379719473 * 5859408629 * 11862763021 * 45767566217

然后 $u,v,w$ 已知，再由
$$
cc \equiv m \cdot w^{r+s} \pmod p \
cb \equiv v^s \pmod p \
ca \equiv u^r \pmod p
$$
我们对 $ca,cb$ 解离散对数就能获取 $s,r$，然后就能计算 $w^{r+s}$，从而解密获取 $m$

exp

1
2
3
4
5
6
7
8
# sage

# 交互获取 cc,cb,ca,p,u,v,w

r = discrete_log(Mod(ca, p), Mod(u, p)) 
s = discrete_log(Mod(cb, p), Mod(v, p))
m = cc * pow(w, -(r + s), p) % p
print(long_to_bytes(m))

PS：这道题能有这么高的分倒是有点不可思议，可能大部分选手没发现 $p-1$ 是光滑的叭。

TinyECC

POINTS：217

考点：椭圆曲线离散对数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
#!/usr/bin/env python3

from mini_ecdsa import *
from Crypto.Util.number import *
from flag import flag

def tonelli_shanks(n, p):
    if pow(n, int((p-1)//2), p) == 1:
            s = 1
            q = int((p-1)//2)
            while True:
                if q % 2 == 0:
                    q = q // 2
                    s += 1
                else:
                    break
            if s == 1:
                r1 = pow(n, int((p+1)//4), p)
                r2 = p - r1
                return r1, r2
            else:
                z = 2
                while True:
                    if pow(z, int((p-1)//2), p) == p - 1:
                        c = pow(z, q, p)
                        break
                    else:
                        z += 1
                r = pow(n, int((q+1)//2), p)
                t = pow(n, q, p)
                m = s
                while True:
                    if t == 1:
                        r1 = r
                        r2 = p - r1
                        return r1, r2
                    else:
                        i = 1
                        while True:
                            if pow(t, 2**i, p) == 1:
                                break
                            else:
                                i += 1
                        b = pow(c, 2**(m-i-1), p)
                        r = r * b % p
                        t = t * b ** 2 % p
                        c = b ** 2 % p
                        m = i
    else:
        return False

def random_point(p, a, b):
    while True:
        gx = getRandomRange(1, p-1)
        n = (gx**3 + a*gx + b) % p
        gy = tonelli_shanks(n, p)
        if gy == False:
            continue
        else:
            return (gx, gy[0])

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, "  Dual ECC means two elliptic curve with same coefficients over the ", border)
    pr(border, "  different fields or ring! You should calculate the discrete log   ", border)
    pr(border, "  in dual ECCs. So be smart in choosing the first parameters! Enjoy!", border)
    pr(border*72)

    bool_coef, bool_prime, nbit = False, False, 128
    while True:
        pr(f"| Options: \n|\t[C]hoose the {nbit}-bit prime p \n|\t[A]ssign the coefficients \n|\t[S]olve DLP \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'a':
            pr('| send the coefficients a and b separated by comma: ')
            COEFS = sc()
            try:
                a, b = [int(_) for _ in COEFS.split(',')]
            except:
                die('| your coefficients are not valid, Bye!!')
            if a*b == 0:
                die('| Kidding me?!! a*b should not be zero!!')
            else:
                bool_coef = True
        elif ans == 'c':
            pr('| send your prime: ')
            p = sc()
            try:
                p = int(p)
            except:
                die('| your input is not valid :(')
            if isPrime(p) and p.bit_length() == nbit and isPrime(2*p + 1):
                q = 2*p + 1
                bool_prime = True
            else:
                die(f'| your integer p is not {nbit}-bit prime or 2p + 1 is not prime, bye!!')
        elif ans == 's':
            if bool_coef == False:
                pr('| please assign the coefficients.')
            if bool_prime == False:
                pr('| please choose your prime first.')
            if bool_prime and bool_coef:
                Ep = CurveOverFp(0, a, b, p)
                Eq = CurveOverFp(0, a, b, q)

                xp, yp = random_point(p, a, b)
                P = Point(xp, yp)

                xq, yq = random_point(q, a, b)
                Q = Point(xq, yq)

                k = getRandomRange(1, p >> 1)
                kP = Ep.mult(P, k)

                l = getRandomRange(1, q >> 1)
                lQ = Eq.mult(Q, l)
                pr('| We know that: ')
                pr(f'| P = {P}')
                pr(f'| k*P = {kP}')
                pr(f'| Q = {Q}')
                pr(f'| l*Q = {lQ}')
                pr('| send the k and l separated by comma: ')
                PRIVS = sc()
                try:
                    priv, qriv = [int(s) for s in PRIVS.split(',')]
                except:
                    die('| your input is not valid, Bye!!')
                if priv == k and qriv == l:
                    die(f'| Congrats, you got the flag: {flag}')
                else:
                    die('| sorry, your keys are not correct! Bye!!!')
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

题目的意思是让你输入系数 $a,b,p$ 来构造一条曲线，然后解一个椭圆曲线上的离散对数问题。

这里有两个思路，一个是构造 $#E_p = p$，使用smart attack，或者 $#E_p = p-1, #E_p = p+1$ 可以使用weil pair 去做。

这里是用smart attack的方法，先根据http://www.monnerat.info/publications/anomalous.pdf生成奇异曲线的参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# http://www.monnerat.info/publications/anomalous.pdf
D = 19
j = -2^15*3^3

def anon_prime(m):
    while True:
        p = (19*m*(m + 1)) + 5
        if is_prime(p):
            return m, p
        m += 1

curves = []
def anom_curve():
    m = 2**61 + 2**60 # chosen so the curves have bit length 128
    while True:
        m, p = anon_prime(m)
        a = (-3*j * inverse_mod((j - 1728), p)) % p
        b = (2*j * inverse_mod((j - 1728), p)) % p
        E = EllipticCurve(GF(p), [a,b]) 
        if E.order() == p:
            G = E.gens()[0]
            if is_prime(2*p + 1):
                print(f'Found an anomalous prime of bit length: {p.nbits()}')
                print(f'Alse q = 2p+1 is a prime. p={p}')
                if p.nbits() != 128:
                    exit()
                curves.append([p,a,b])
                #print(curves)
        m += 1
anom_curve()

对于第一条曲线我们就可以用smart attack进行离散对数的求解了，

那么第二条曲线，我们就遍历一下，尽量找一条比较光滑的曲线，以便直接使用pohlig-hellman对其继续离散对数求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
for param in curves:
    p, a, b = param
    q = 2*p + 1
    E1 = EllipticCurve(GF(p), [a,b])
    E2 = EllipticCurve(GF(q), [a,b])
    assert E1.order() == p
    if factor(E2.order())[-1][0] <= 2^32:
        print(factor(E2.order()))
        print(p)

# 2 * 11 * 29 * 269 * 809 * 1153 * 5527 * 1739687 * 272437559 * 1084044811
# 227297987279223760839521045903912023553
# 2^12 * 3^2 * 5^2 * 3943 * 417869 * 2117447 * 204521147 * 691298191
# 227297987279232780301248910046242203569
# 3^3 * 5 * 233 * 241 * 17473333 * 57368039 * 57798431 * 1035039791
# 227297987279245567422831795384518183819

一个例子

1
2
3
4
5
# E2.order() = 2 * 11 * 29 * 269 * 809 * 1153 * 5527 * 1739687 * 272437559 * 1084044811
p = 227297987279223760839521045903912023553
q = 2*p + 1
a = 120959747616429018926294825597988269841 
b = 146658155534937748221991162171919843659

然后进行 smart attack 和 discrete_log

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

p = 227297987279223760839521045903912023553
q = 2*p + 1
a = 120959747616429018926294825597988269841 
b = 146658155534937748221991162171919843659

Ep = EllipticCurve(GF(p), [a,b])
G = Ep(97161828186858857945099901434400040095,76112161730436240110429589963792144699)
rG = Ep(194119107523766318610516779439078452539,111570625156450061932127850545534033820)

print(SmartAttack(G,rG,p))

Eq = EllipticCurve(GF(q), [a,b])
H = Eq(229869041108862357437180702478501205702,238550780537940464808919616209960416466)
sH = Eq(18599290990046241788386470878953668775,281648589325596060237553465951876240185)

print(H.discrete_log(sH))

交互拿到flag：CCTF{ECC_With_Special_Prime5}

不过还有比较简单的方法（也许是非预期），这里只检查了 $a\cdot b = 0?$ 而不是在模 $p$ 下，所以这里可以绕过，从而构造一条奇异曲线 $y^2 \equiv x^3 \pmod p$

这样就有同态 $E(x,y) \to \frac{x}{y}$，离散对数解起来就很方便了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
p = 227297987279223760839521045903912023553
q = 2*p + 1

Fp = GF(p)
Fq = GF(q)

Px, Py = (171267639996301888897655876215740853691,17515108248008333086755597522577521623)
kPx, kPy = (188895340186764942633236645126076288341,83479740999426843193232746079655679683)
k = Fp(Fp(kPx) / Fp(kPy)) / Fp(Fp(Px) / Fp(Py))

Qx, Qy = (297852081644256946433151544727117912742,290511976119282973548634325709079145116)
lQx, lQy = (83612230453021831094477443040279571268,430089842202788608377537684275601116540)
l = Fq(Fq(lQx) / Fq(lQy)) / Fq(Fq(Qx) / Fq(Qy))

print(f'{k}, {l}')

以上脚本来自https://blog.cryptohack.org/cryptoctf2021-hard#tiny-ecc

ELEGANT CURVE

POINTS：217

考点：椭圆曲线离散对数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
from Crypto.Util.number import *
import sys
from flag import flag

def tonelli_shanks(n, p):
    if pow(n, int((p-1)//2), p) == 1:
            s = 1
            q = int((p-1)//2)
            while True:
                if q % 2 == 0:
                    q = q // 2
                    s += 1
                else:
                    break
            if s == 1:
                r1 = pow(n, int((p+1)//4), p)
                r2 = p - r1
                return r1, r2
            else:
                z = 2
                while True:
                    if pow(z, int((p-1)//2), p) == p - 1:
                        c = pow(z, q, p)
                        break
                    else:
                        z += 1
                r = pow(n, int((q+1)//2), p)
                t = pow(n, q, p)
                m = s
                while True:
                    if t == 1:
                        r1 = r
                        r2 = p - r1
                        return r1, r2
                    else:
                        i = 1
                        while True:
                            if pow(t, 2**i, p) == 1:
                                break
                            else:
                                i += 1
                        b = pow(c, 2**(m-i-1), p)
                        r = r * b % p
                        t = t * b ** 2 % p
                        c = b ** 2 % p
                        m = i
    else:
        return False

def add(A, B, p):
    if A == 0:
        return B
    if B == 0:
        return A
    l = ((B[1] - A[1]) * inverse(B[0] - A[0], p)) % p
    x = (l*l - A[0] - B[0]) % p
    y = (l*(A[0] - x) - A[1]) % p
    return (int(x), int(y))

def double(G, a, p):
    if G == 0:
        return G
    l = ((3*G[0]*G[0] + a) * inverse(2*G[1], p)) % p
    x = (l*l - 2*G[0]) % p
    y = (l*(G[0] - x) - G[1]) % p
    return (int(x), int(y))

def multiply(point, exponent, a, p):
    r0 = 0
    r1 = point
    for i in bin(exponent)[2:]:
        if i == '0':
            r1 = add(r0, r1, p)
            r0 = double(r0, a, p)
        else:
            r0 = add(r0, r1, p)
            r1 = double(r1, a, p)
    return r0

def random_point(a, b, p):
    while True:
        x = getRandomRange(1, p-1)
        try:
            y, _ = tonelli_shanks((x**3 + a*x + b) % p, p)
            return (x, y)
        except:
            continue

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, " hi talented cryptographers, the mission is decrypt a secret message", border)
    pr(border, " with given parameters for two elliptic curve, so be genius and send", border)
    pr(border, " suitable parameters, now try to get the flag!                      ", border)
    pr(border*72)

    nbit = 160

    while True:
        pr("| Options: \n|\t[S]end ECC parameters and solve the task \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 's':
            pr("| Send the parameters of first ECC y^2 = x^3 + ax + b like: a, b, p ")
            params = sc()
            try:
                a, b, p = params.split(',')
                a, b, p = int(a), int(b), int(p)
            except:
                die("| your parameters are not valid!!")
            if isPrime(p) and 0 < a < p and 0 < b < p and p.bit_length() == nbit:
                pr("| Send the parameters of second ECC y^2 = x^3 + cx + d like: c, d, q ")
                pr("| such that 0 < q - p <= 2022")
                params = sc()
                try:
                    c, d, q = params.split(',')
                    c, d, q = int(c), int(d), int(q)
                except:
                    die("| your parameters are not valid!!")
                if isPrime(q) and 0 < c < q and 0 < d < q and 0 < q - p <= 2022 and q.bit_length() == nbit:
                    G, H = random_point(a, b, p), random_point(c, d, q)
                    r, s = [getRandomRange(1, p-1) for _ in range(2)]
                    pr(f"| G is on first  ECC and G =", {G})
                    pr(f"| H is on second ECC and H =", {H})
                    U = multiply(G, r, a, p)
                    V = multiply(H, s, c, q)
                    pr(f"| r * G =", {U})
                    pr(f"| s * H =", {V})
                    pr("| Send r, s to get the flag: ")
                    rs = sc()
                    try:
                        u, v = rs.split(',')
                        u, v = int(u), int(v)
                    except:
                        die("| invalid input, bye!")
                    if u == r and v == s:
                        die("| You got the flag:", flag)
                    else:
                        die("| the answer is not correct, bye!")
                else:
                    die("| invalid parameters, bye!")
            else:
                die("| invalid parameters, bye!")
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

和上面的差不多，不过这次要输入两条曲线各自的 $a,b,p$，也限制了$p-q<2022,$ $a,b,c,d$ 也必须是大于 $0$，小于 $p$ 或者 $q$ 的，这样我们就不能用 $a=b=0$ 或者是 $a,b = kp$ 这样去构造奇异曲线 $y^2 \equiv x^3 \pmod p$ 了，那就还是用TinyECC那边的smartattack叭，找到一条奇异曲线，然后设 $q = nextprme(p)$，再改变合适的系数使得 $#Eq$ 是光滑的（前面是变 $q$，这里是变 $a,b$，都大差不差的），这样离散对数好求。

下面是一组示例

1
2
3
4
5
6
7
q = 730750818665451459112596905638433048232067472077
aq = 3
bq = 481
Eq = EllipticCurve(GF(q), [aq,bq])

factor(Eq.order())                                                                                                
2^2 * 3 * 167 * 193 * 4129 * 882433 * 2826107 * 51725111 * 332577589 * 10666075363
1
2
3
4
5
6
p = 730750818665451459112596905638433048232067471723 
ap = 425706413842211054102700238164133538302169176474 
bp = 203362936548826936673264444982866339953265530166
q = 730750818665451459112596905638433048232067472077
aq = 3
bq = 481
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from random import getrandbits

# params from http://www.monnerat.info/publications/anomalous.pdf
D = 11
j = -2**15

def anom_curve():
    m = 257743850762632419871495
    p = (11*m*(m + 1)) + 3
    a = (-3*j * inverse_mod((j - 1728), p)) % p
    b = (2*j * inverse_mod((j - 1728), p)) % p
    E = EllipticCurve(GF(p), [a,b])
    G = E.gens()[0]
    return p, a, b, E, G

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)


p = 730750818665451459112596905638433048232067471723 
ap = 425706413842211054102700238164133538302169176474 
bp = 203362936548826936673264444982866339953265530166

Ep = EllipticCurve(GF(p), [ap,bp])
G = Ep(126552689249226752349356206494226396414163660811, 559777835342379827315577715664975494598512818777)
rG = Ep(190128385937465835164338802317889165657442536853, 604514027124204305317929024826237325074492980218)

print(SmartAttack(G,rG,p))

q = 730750818665451459112596905638433048232067472077
aq = 3
bq = 481
Eq = EllipticCurve(GF(q), [aq,bq])

H = Eq(284866865619833057500909264169831974815120720320, 612322665682105897045018564282609259776516527853)
sH = Eq(673590124165798818844330235458561515292416807353, 258709088293250578320930080839442511989120686226)

print(H.discrete_log(sH))

flag: CCTF{Pl4yIn9_Wi7H_ECC_1Z_liK3_pLAiNg_wiTh_Fir3!!}

PS：感觉这两道题也可以控制参数使得两条曲线的阶都是比较光滑的，然后再解离散对数？

DOUBLE MIFF

POINTS：217

考点：椭圆曲线与丢番图方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from Crypto.Util.number import *
from secret import a, b, p, P, Q
from flag import flag

def onmiff(a, b, p, G):
    x, y = G
    return (a*x*(y**2 - 1) - b*y*(x**2 - 1)) % p == 0

def addmiff(X, Y):
    x_1, y_1 = X
    x_2, y_2 = Y
    x_3 = (x_1 + x_2) * (1 + y_1*y_2) * inverse((1 + x_1*x_2) * (1 - y_1*y_2), p) % p
    y_3 = (y_1 + y_2) * (1 + x_1*x_2) * inverse((1 + y_1*y_2) * (1 - x_1*x_2), p) % p
    return (x_3, y_3)


l = len(flag) // 2
m1, m2 = bytes_to_long(flag[:l]), bytes_to_long(flag[l:])

assert m1 < (p // 2) and m2 < (p // 2)
assert onmiff(a, b, p, P) and onmiff(a, b, p, Q)
assert P[0] == m1 and Q[0] == m2

print(f'P + Q = {addmiff(P, Q)}')
print(f'Q + Q = {addmiff(Q, Q)}')
print(f'P + P = {addmiff(P, P)}')
P + Q = (540660810777215925744546848899656347269220877882, 102385886258464739091823423239617164469644309399)
Q + Q = (814107817937473043563607662608397956822280643025, 961531436304505096581595159128436662629537620355)
P + P = (5565164868721370436896101492497307801898270333, 4969213281060625285080264123281718864612235

根据题目我们有曲线 $ax(y^2 - 1)\equiv by(x^2-1) \pmod p$，其中曲线参数 $a,b,p$ 均未知，但是我们有 $P+P,Q+Q,P+Q$，$p$ 总是要恢复的叭，需要用到给出的三个点。那么通过这三个点，我们有等式 $(P+P) + (Q+Q) = 2 \cdot (P+Q)$，我们设 $2\cdot (P+Q)=(x_0,y_0),P+Q=(x_1,y_1),Q+Q=(x_2,y_2),P+P=(x_3,y_3)$，那么我们有
$$
x_0 \equiv \frac{(x_2+x_3)\cdot(1+y_2y_3)}{(1+x_2x_3)(1-y_2y_3)} \pmod p
$$

$$
x_0 \equiv \frac{2x_1(1+y_1^2)}{(1+x_1^2)(1-y_1^2)} \pmod p
$$

两式相减我们有
$$
(x_2+x_3)\cdot(1+y_2y_3) \cdot (1+x_1^2)(1-y_1^2)-2x_1(1+y_1^2)\cdot(1+x_2x_3)(1-y_2y_3) \equiv 0 \pmod p
$$
同理，由 $y$ 坐标的计算公式我们可以得到
$$
(y_2+y_3)\cdot(1+x_2x_3) \cdot (1+y_1^2)(1-x_1^2)-2y_1(1+x_1^2)\cdot(1+y_2y_3)(1-x_2x_3) \equiv 0 \pmod p
$$
两个模 $p$ 同余 $0$ 式子，我们求一个 $gcd$ 就能获取 $p$ 的一个倍数了，分解一下应该就能获取素数 $p$。

回到曲线的式子 $ax(y^2-1) \equiv by(x^2-1)$，对于两个未知数，emmm，我们给他搞成一个先 ，故而有
$$
k \equiv \frac{a}{b} \equiv \frac{y(x^2-1)}{x(y^2-1)}
$$
于是只需要一个点我们就能知道 $k \equiv \frac {a}{b}$，换一换也有
$$
k\frac{x}{x^2-1} \equiv \frac{y}{y^2-1}
$$
我们设 $P=(x_4,y_4)$，那么根据加法规则，我们有
$$
x_3 \equiv \frac{2x_4(1+y_4^2)}{(1+x_4^2)(1-y_4^2)} \pmod p
$$

$$
y_3 \equiv \frac{2y_4(1+x_4^2)}{(1+y_4^2)(1-x_4^2)} \pmod p
$$

两式相乘，我们有
$$
x_3y_3 \equiv \frac{4x_4y_4}{(x_4^2-1)(y_4^2-1)} \equiv 4k(\frac{x_4}{x_4^2-1})^2 \pmod p
$$
于是我们有
$$
(\frac{x_4^2-1}{x_4})^2 \equiv \frac{4k}{x_3y_3} \pmod p
$$
因为 $p \equiv 3 \pmod 4$，于是我们设 $l \equiv (\frac{4k}{x_3y_3})^{\frac{p+1}{4}}$，则有 $\frac{x_4^2-1}{x_4} \equiv \pm l$

于是我们有 $-x_4^2 \pm lx_4 +1 \equiv 0\pmod p$，解一手二次方程，$x \equiv \frac{\mp l \pm \sqrt{l^2+4}}{2}$ ，我们就能够拿到 $P$ 啦，同理也可以这么去拿$Q$，然后就能恢复 flag了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#!/usr/bin/env python3
from Crypto.Util.number import isPrime, long_to_bytes
from math import gcd

x1, y1 = (540660810777215925744546848899656347269220877882, 102385886258464739091823423239617164469644309399)
x2, y2 = (814107817937473043563607662608397956822280643025, 961531436304505096581595159128436662629537620355)
x3, y3 = (5565164868721370436896101492497307801898270333, 496921328106062528508026412328171886461223562143)
num1 = (1 + x1 ** 2) * (1 - y1 ** 2) * (x2 + x3) * (1 + y2 * y3) - 2 * x1 * (1 + y1 ** 2) * (1 + x2 * x3) * (1 - y2 * y3)
num2 = (1 + y1 ** 2) * (1 - x1 ** 2) * (y2 + y3) * (1 + x2 * x3) - 2 * y1 * (1 + x1 ** 2) * (1 + y2 * y3) * (1 - x2 * x3)
pmult = gcd(num1, num2)
print(pmult)
# sage: factor(9132984636916703206790144643146359197427822823096)
# 2^3 * 1141623079614587900848768080393294899678477852887

p=1141623079614587900848768080393294899678477852887
def recover_half(x, y):
    k = y * (x ** 2 - 1) * pow(x * (y ** 2 - 1), -1, p) % p
    l = pow(4 * k * pow(x * y, -1, p), (p + 1) // 4, p)
    D = (l ** 2 + 4) % p
    sqrtD = pow(D, (p + 1) // 4, p)
    for i in (-1, 1):
        for j in (-1, 1):
            num = (i * l + j * sqrtD) * pow(2, -1, p) % p
            text = long_to_bytes(num)
            if b'CCTF{' in text or b'}' in text:
                return text

first_half = recover_half(x3, y3)
second_half = recover_half(x2, y2)
flag = (first_half + second_half).decode()
print(flag)
#CCTF{D39enEr47E_ECC_4TtaCk!_iN_Huffs?}

ECCHIMERA

POINTS：271

考点：椭圆曲线离散对数，smart attack，pohlig-hellman

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sage.all import *
from flag import flag


n = 43216667049953267964807040003094883441902922285265979216983383601881964164181
U = 18230294945466842193029464818176109628473414458693455272527849780121431872221
V = 13100009444194791894141652184719316024656527520759416974806280188465496030062
W = 5543957019331266247602346710470760261172306141315670694208966786894467019982

flag = flag.lstrip(b'CCTF{').rstrip(b'}')
s = int(flag.hex(), 16)
assert s < n

E = EllipticCurve(Zmod(n), [0, U, 0, V, W])
G = E(6907136022576092896571634972837671088049787669883537619895520267229978111036, 35183770197918519490131925119869132666355991678945374923783026655753112300226)

print(f'G = {G}')
print(f's * G = {s * G}')

n可以分解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
n = 43216667049953267964807040003094883441902922285265979216983383601881964164181
U = 18230294945466842193029464818176109628473414458693455272527849780121431872221
V = 13100009444194791894141652184719316024656527520759416974806280188465496030062
W = 5543957019331266247602346710470760261172306141315670694208966786894467019982

E = EllipticCurve(Zmod(n), [0, U, 0, V, W])
G = E(6907136022576092896571634972837671088049787669883537619895520267229978111036, 35183770197918519490131925119869132666355991678945374923783026655753112300226)
sG = E(14307615146512108428634858855432876073550684773654843931813155864728883306026, 4017273397399838235912099970694615152686460424982458188724369340441833733921)

p = 190116434441822299465355144611018694747
q = 227316839687407660649258155239617355023

assert p * q == n

# P and Q curves
Ep = EllipticCurve(GF(p), [0, ZZ(U % p), 0, ZZ(V % p), ZZ(W % p)])
Eq = EllipticCurve(GF(q), [0, ZZ(U % q), 0, ZZ(V % q), ZZ(W % q)])

kp = Ep.order()
kq = Eq.order()

第一部分

kp=p，smart attack

第二部分

sage: factor(kq)
2^4 * 3 * 13 * 233 * 4253 * 49555349 * 7418313402470596923151

但是直接discrete_log好像不行，这里选择放弃因子 3（Gq的阶没有因子3） 和 最大的 7418313402470596923151（数值太大） ，然后手撸一个pohlig hellman （也可以调参调用discrete_log，但好慢，感觉不如手撸）

1
2
3
4
5
6
7
8
9
10
11
primes = [2^4,13, 233, 4253, 49555349] #don't use 3 and last one, cuz last one is too big, and 3 is not Gq's order's factor
dlogs = []

for fac in primes:
    print(fac)
    t = int(Gq.order()) // int(fac)
    dlog = (t*Gq).discrete_log(t*sGq) #discrete_log(t*sGq, t*Gq, operation="+")
    dlogs += [dlog]
    #print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order

q_secret = crt(dlogs, primes)

最后再crt一下就好了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#!/usr/bin/env sage
from Crypto.Util.number import *

n = 43216667049953267964807040003094883441902922285265979216983383601881964164181
U = 18230294945466842193029464818176109628473414458693455272527849780121431872221
V = 13100009444194791894141652184719316024656527520759416974806280188465496030062
W = 5543957019331266247602346710470760261172306141315670694208966786894467019982

E = EllipticCurve(Zmod(n), [0, U, 0, V, W])
G = E(6907136022576092896571634972837671088049787669883537619895520267229978111036, 35183770197918519490131925119869132666355991678945374923783026655753112300226)
sG = E(14307615146512108428634858855432876073550684773654843931813155864728883306026, 4017273397399838235912099970694615152686460424982458188724369340441833733921)

p = 190116434441822299465355144611018694747
q = 227316839687407660649258155239617355023

assert p * q == n

# P curve
Ep = EllipticCurve(GF(p), [0, ZZ(U % p), 0, ZZ(V % p), ZZ(W % p)])
Eq = EllipticCurve(GF(q), [0, ZZ(U % q), 0, ZZ(V % q), ZZ(W % q)])

kp = Ep.order()
kq = Eq.order()

Gp = Ep(6907136022576092896571634972837671088049787669883537619895520267229978111036, 35183770197918519490131925119869132666355991678945374923783026655753112300226)
Gq = Eq(6907136022576092896571634972837671088049787669883537619895520267229978111036, 35183770197918519490131925119869132666355991678945374923783026655753112300226)

sGp = Ep(14307615146512108428634858855432876073550684773654843931813155864728883306026, 4017273397399838235912099970694615152686460424982458188724369340441833733921)
sGq = Eq(14307615146512108428634858855432876073550684773654843931813155864728883306026, 4017273397399838235912099970694615152686460424982458188724369340441833733921)

print(Gp.order())
print(Gq.order())

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

primes = [2^4, 13, 233, 4253, 49555349] #don't use 3 and last one
dlogs = []

for fac in primes:
    t = int(Gq.order()) // int(fac)
    dlog = (t*Gq).discrete_log(t*sGq) #discrete_log(t*sGq, t*Gq, operation="+")
    dlogs += [dlog]
    #print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order


p_secret = SmartAttack(Gp,sGp,p)
q_secret = crt(dlogs, primes)  #9092500866606561 #discrete_log(sGq, Gq, ord=Gq.order(), bounds=2^4 * 13 * 233 * 4253 * 49555349, operation="+")

print(p_secret, q_secret)
flag = long_to_bytes(int(crt([p_secret, q_secret], [Gp.order(), Gq.order() // 7418313402470596923151])))
print(flag)

flag:CCTF{m1X3d_VeR5!0n_oF_3Cc!}

主要因为 $flag < Gp.order \cdot Gq.order / 7418313402470596923151 $ ，所以我们才能解出flag。

ROHALD

POINTS：180

考点：椭圆曲线、Edwards Curve、Montgomery、Weierstrass

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#!/usr/bin/env sage

from Crypto.Util.number import *
from secret import flag, Curve

def ison(C, P):
    c, d, p = C
    u, v = P
    return (u**2 + v**2 - c**2 * (1 + d * u**2*v**2)) % p == 0

def teal(C, P, Q):
    c, d, p = C
    u1, v1 = P
    u2, v2 = Q
    assert ison(C, P) and ison(C, Q)
    u3 = (u1 * v2 + v1 * u2) * inverse(c * (1 + d * u1 * u2 * v1 * v2), p) % p
    v3 = (v1 * v2 - u1 * u2) * inverse(c * (1 - d * u1 * u2 * v1 * v2), p) % p
    return (int(u3), int(v3))

def peam(C, P, m):
    assert ison(C, P)
    c, d, p = C
    B = bin(m)[2:]
    l = len(B)
    u, v = P
    PP = (-u, v)
    O = teal(C, P, PP)
    Q = O
    if m == 0:
        return O
    elif m == 1:
        return P
    else:
        for _ in range(l-1):
            P = teal(C, P, P)
        m = m - 2**(l-1)
        Q, P = P, (u, v)
        return teal(C, Q, peam(C, P, m))

c, d, p = Curve

flag = flag.lstrip(b'CCTF{').rstrip(b'}')
l = len(flag)
lflag, rflag = flag[:l // 2], flag[l // 2:]

s, t = bytes_to_long(lflag), bytes_to_long(rflag)
assert s < p and t < p

P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)

print(f'ison(C, P) = {ison(Curve, P)}')
print(f'ison(C, Q) = {ison(Curve, Q)}')

print(f'P = {P}')
print(f'Q = {Q}')

print(f's * P = {peam(Curve, P, s)}')
print(f't * Q = {peam(Curve, Q, t)}')

ison(C, P) = True
ison(C, Q) = True
P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)
s * P = (730393937659426993430595540476247076383331, 461597565155009635099537158476419433012710)
t * Q = (500532897653416664117493978883484252869079, 620853965501593867437705135137758828401933)

首先还是要获取椭圆曲线的参数 $c,d,p$

对于 $p$ 的获取，由于我们知道四个点 $P,Q,sP,tQ$

根据曲线我们有 $x^2+y^2 \equiv c^2(1+dx^2y^2) \pmod p$

所以如果有两个点，我们就能够得出 $c^2d$

$X_1 = x_1^2 +y_1^2-c^2(1+dx_1^2y_1^2) = k_1p$

$X_2 = x_2^2 +y_2^2-c^2(1+dx_2^2y_2^2) = k_2p$

两式相减我们有 $X_1-X_2 = (x_1^2+y_1^2-x_2^2-y_2^2)-c^2d(x_1^2y_1^2-x_2^2y_2^2) = (k_1-k_2)p \equiv 0 \pmod p$

于是 $c^2d \equiv \frac{(x_1^2+y_1^2-x_2^2-y_2^2)}{x_1^2y_1^2-x_2^2y_2^2} \pmod p$ ，可求

有了 $c^2d$，我们就能求出 $X_1-X_2=(k_1-k_2)p$ 了，

同理我们用另外两个点就能够搞出 $X_3-X_4 = (k_3-k_4)p$ 了，然后 gcd一下，再factor一下，就能够求出 $p$ 了。

有了$c^2d$，根据 $X_1 = x_1^2 +y_1^2-c^2(1+dx_1^2y_1^2) \equiv 0 \pmod p$ 也能求出 $c^2$ 了，从而也能求出 $d$ 了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
from math import gcd

def ison(C, P):
    """
    Verification points are on the curve
    """
    c, d, p = C
    u, v = P
    return (u**2 + v**2 - cc * (1 + d * u**2*v**2)) % p == 0

def a_and_b(u1,u2,v1,v2):
    """
    Helper function used to simplify calculations
    """
    a12 = u1**2 - u2**2 + v1**2 - v2**2
    b12 = u1**2 * v1**2 - u2**2 * v2**2
    return a12, b12

def find_modulus(u1,u2,u3,u4,v1,v2,v3,v4):
    """
    Compute the modulus from four points
    """
    a12, b12 = a_and_b(u1,u2,v1,v2)
    a13, b13 = a_and_b(u1,u3,v1,v3)
    a23, b23 = a_and_b(u2,u3,v2,v3)
    a24, b24 = a_and_b(u2,u4,v2,v4)

    p_almost = gcd(a12*b13 - a13*b12, a23*b24 - a24*b23)

    for i in range(2,1000):
        if p_almost % i == 0:
            p_almost = p_almost // i

    return p_almost

def c_sq_d(u1,u2,v1,v2,p):
    """
    Helper function to computer c^2 d
    """
    a1,b1 = a_and_b(u1,u2,v1,v2)
    return a1 * pow(b1,-1,p) % p

def c(u1,u2,v1,v2,p):
    """
    Compute c^2, d from two points and known modulus
    """
    ccd = c_sq_d(u1,u2,v1,v2,p)
    cc = (u1**2 + v1**2 - ccd*u1**2*v1**2) % p
    d = ccd * pow(cc, -1, p) % p
    return cc, d


P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)
sP = (730393937659426993430595540476247076383331, 461597565155009635099537158476419433012710)
tQ = (500532897653416664117493978883484252869079, 620853965501593867437705135137758828401933)

u1, v1 = P
u2, v2 = Q
u3, v3 = sP
u4, v4 = tQ

p = find_modulus(u1,u2,u3,u4,v1,v2,v3,v4)
cc, d = c(u1,u2,v1,v2,p)

C = cc, d, p
assert ison(C, P)
assert ison(C, Q)
assert ison(C, sP)
assert ison(C, tQ)

print(f'Found curve parameters')
print(f'p = {p}')
print(f'c^2 = {cc}')
print(f'd = {d}')

# Found curve
# p = 903968861315877429495243431349919213155709
# cc = 495368774702871559312404847312353912297284
# d = 540431316779988345188678880301417602675534

脚本来自https://blog.cryptohack.org/cryptoctf2021-hard#rohald（注意 $c^2$ 开根的时候有两个解，最后解flag的时候都要尝试一下）

然后我们得转化这个椭圆曲线的形式，从Edwards Curve 转到 Montgomery形式最后变成Weierstrass形式，然后会发现这条曲线的阶光滑，直接调用 sagemath 的 discrete_log 就能进行求解。

$E_{c,d} : u^2 + v^2 -c^2 (1+du^2v^2)=0$

$u_{P+Q} = \frac{(u_Pv_Q)+(v_Pu_Q)}{c(1+du_Pu_Qv_Pv_Q)}$

$v_{P+Q}=\frac{(-u_Pv_Q)+(v_Pu_Q)}{c(1-du_Pu_Qv_Pv_Q)}$

Edwards Curve to $u’^2 + v’^2 =1+d’u’^2v’^2$ $(d’=dc^4,u’ = \frac{u}{c},v’=\frac{v}{c})$

to Montgomery $By’^2=x’^3+Ax’^2+x$ $(x’=\frac{1+v’}{1-v’},y’=\frac{2(1+v’)}{u’(1-v’)},A=\frac{2(1+d’)}{1-d’},B = \frac{1}{1-d’})$

to Weierstrass $y^2 =x^3 +ax+b$ $(x = \frac{x’}{B}+\frac{A}{3B},y=\frac{y’}{B},a=\frac{3-A^2}{3B^2},b=\frac{2A^3-9A}{27B^3})$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def to_elliptic_2(P, p, c, d):
    Zp = Zmod(p)
    x, y = P
    x, y = Zp(x), Zp(y)
    c, d = Zp(c), Zp(d)
    x, y = x / c , y / c 
    d = d * c ** 4
    
    # Montgomery
    u = (1 + y) / (1 - y)
    v = (2 * (1+y)) / (x * (1-y))
    B = 1 / (1-d)
    A = 2 * (1+d) / (1-d)

    # Weierstrass
    x = u / B + A / (3*B)
    y = v / B
    a = (3 - A**2) / (3 * B**2)
    b = (2 * A**3 - 9*A) / (27 * B**3)
    return (x, y), a, b

p = 903968861315877429495243431349919213155709
c = 662698094423288904843781932253259903384619
d = 540431316779988345188678880301417602675534
P = (398011447251267732058427934569710020713094, 548950454294712661054528329798266699762662)
Q = (139255151342889674616838168412769112246165, 649791718379009629228240558980851356197207)
S = (730393937659426993430595540476247076383331, 461597565155009635099537158476419433012710)
T = (500532897653416664117493978883484252869079, 620853965501593867437705135137758828401933)

P1, a, b = to_elliptic_2(P, p, c, d)
Q1, a, b = to_elliptic_2(Q, p, c, d)
S1, a, b = to_elliptic_2(S, p, c, d)
T1, a, b = to_elliptic_2(T, p, c, d)

EC = EllipticCurve(Zmod(p), [a, b])
P1 = EC(P1)
Q1 = EC(Q1)
S1 = EC(S1)
T1 = EC(T1)

s = P1.discrete_log(S1)
t = Q1.discrete_log(T1)
print(s)
print(t)

脚本来自 https://zhuanlan.zhihu.com/p/399487467

ROBERT

POINTS：194

考点： carmichael_lambda

1
2
3
4
5
6
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+   hi all, all cryptographers know that fast calculation is not easy! +
+   In each stage for given integer m, find number n such that:        +
+   carmichael_lambda(n) = m, e.g. carmichael_lambda(2021) = 966       +
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
| send an integer n such that carmichael_lambda(n) = 52:

给出一个值 $s$，求 $lcm(n)=s$ 的 $n$，一个想法是通过查找 $s$ 的因子 $x,y$， 如果 $x+1,y+1$ 为素数，并且满足 $lcm(x,y)=s$，那么我们有 $n = (x+1)\cdot(y+1)$

1
2
3
4
5
def reverse_lambda(n):
    for x in divisors(n):
        for y in divisors(n):
            if lcm(x, y) == n and is_prime(x + 1) and is_prime(y + 1):
                return (x + 1) * (y + 1)

TRUNC

POINTS：334

考点：Signature forgery

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#!/usr/bin/env python3

from Crypto.Util.number import *
from hashlib import sha256
import ecdsa
from flag import FLAG

E = ecdsa.SECP256k1
G, n = E.generator, E.order

cryptonym = b'Persian Gulf'

def keygen(n, G):
    privkey = getRandomRange(1, n-1)
    pubkey = privkey * G
    return (pubkey, privkey)

def sign(msg, keypair):
    nbit, dbit = 256, 25
    pubkey, privkey = keypair
    privkey_bytes = long_to_bytes(privkey)
    x = int(sha256(privkey_bytes).hexdigest(), 16) % 2**dbit
    while True:
        k, l = [(getRandomNBitInteger(nbit) << dbit) + x for _ in '01']
        u, v = (k * G).x(), (l * G).y()
        if u + v > 0:
            break
    h = int(sha256(msg).hexdigest(), 16)
    s = inverse(k, n) * (h * u - v * privkey) % n
    return (int(u), int(v), int(s))

def verify(msg, pubkey, sig):
    if any(x < 1 or x >= n for x in sig):
        return False
    u, v, s = sig
    h = int(sha256(msg).hexdigest(), 16)
    k, l = h * u * inverse(s, n), v * inverse(s, n)
    X = (k * G + (n - l) * pubkey).x()
    return (X - u) % n == 0

def die(*args):
    pr(*args)
    quit()

def pr(*args):
    s = " ".join(map(str, args))
    sys.stdout.write(s + "\n")
    sys.stdout.flush()

def sc():
    return sys.stdin.readline().strip()

def main():
    border = "+"
    pr(border*72)
    pr(border, " hi all, welcome to the high secure elliptic curve signature oracle!", border)
    pr(border, " Your mission is to sign the out cryptonym, try your best :)        ", border)
    pr(border*72)

    keypair = keygen(n, G)
    pubkey, privkey = keypair

    while True:
        pr("| Options: \n|\t[P]rint the pubkey \n|\t[S]ign \n|\t[V]erify \n|\t[Q]uit")
        ans = sc().lower()
        if ans == 'p':
            pr("| pubkey =", pubkey.x(), pubkey.y())
        elif ans == 's':
            pr("| send your hex message to sign: ")
            msg = sc()
            try:
                msg = bytes.fromhex(msg)
            except:
                die("| your message is not valid! Bye!!")
            if msg == cryptonym:
                die('| Kidding me? Bye')
            msg = msg[:14]
            sig = sign(msg, keypair)
            pr("| sign =", sig)
        elif ans == 'v':
            pr("| send your hex message to verify: ")
            msg = sc()
            try:
                msg = bytes.fromhex(msg)
            except:
                die("| your message is not valid! Bye!!")
            pr("| send the signature separated with comma: ")
            sig = sc()
            try:
                sig = [int(s) for s in sig.split(',')]
            except:
                die("| your signature is not valid! Bye!!")
            if verify(msg, pubkey, sig):
                if msg == cryptonym:
                    die("| Good job! Congrats, the flag is:", FLAG)
                else:
                    pr("| your message is verified!!")
            else:
                die("| your signature is not valid! Bye!!")
        elif ans == 'q':
            die("Quitting ...")
        else:
            die("Bye ...")

if __name__ == '__main__':
    main()

可以被非预期，

注意到验签函数：$k = hus^{-1},l=v\cdot s^{-1}$，其中$u,v,s$ 可控，验证 $(kG+(n-l)P)_x\equiv u \pmod n$

若目标消息哈希为 $h$，我们构造任意消息哈希为 $h’$，并且设 $m \equiv \frac{h}{h’} \pmod n$，

随后我们让服务端签名我们的消息，并得到签名 $u’,v’,s’$，此时 $k’=h’u’s’^{-1},l’=v’\cdot s’^{-1}$，该组 $(k,l)$能通过验证。

那么我们在伪造签名时只要设 $u=u’,s=s’m,v=v’m$，

就会有 $k = h’mu’(s’m)^{-1}=h’u’s’^{-1},l=v’m(s’m)^{-1}=v’s’^{-1}$，由上可知，该组 $(k,l)$ 能通过验证。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#!/usr/bin/env python3
from pwn import remote
from ecdsa import SECP256k1
from hashlib import sha256

n = SECP256k1.order
m1 = b'lol' # any other message is fine
m2 = b'Persian Gulf'
h1 = int(sha256(m1).hexdigest(), 16)
h2 = int(sha256(m2).hexdigest(), 16)
m = h2 * pow(h1, -1, n) % n
r = remote("02.cr.yp.toc.tf", 23010)
for _ in range(9):
    r.recvline()
r.sendline('s')
r.recvline()
r.sendline(m1.hex())
u1, v1, w1 = eval(r.recvline()[8:])
u2, v2, w2 = u1, v1 * m % n, w1 * m % n
for _ in range(5):
    r.recvline()
r.sendline('v')
r.recvline()
r.sendline(m2.hex())
r.recvline()
r.sendline(','.join(map(str, [u2, v2, w2])))
print(r.recvline().decode().strip().split()[-1])
r.close()

CCTF{__ECC_Bi4seD_N0nCE_53ns3_LLL!!!}

（PS：不过看着flag，估计要构造格，又非预期了，，，）

MY SIEVE

POINTS：477

考点：RSA

1
2
3
4
5
6
7
8
enc = 17774316754182701043637765672766475504513144507864625935518462040899856505354546178499264702656639970102754546327338873353871389580967004810214134215521924626871944954513679198245322915573598165643628084858678915415521536126034275104881281802618561405075363713125886815998055449593678564456363170087233864817

-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCB*QKBgQCkRgRCyTcSwlBKmERQV/BHkurS
5QnYz7Rm18OjxuuWT3A*Ueqzq7fHISey2NEEtral/*E7v2Dy59DYHoRAAouWQd03
ZYWnvU5mWoYRcpNmHIj8q*+FOtBWcCGzMZ8uxOxaV74vqqerjxyRI14rXZ+QOcNM
/TMM84h0rl/IKqqWsQIDAQAB
-----END PUBLIC KEY-----

题目还给了一个msieve文件，里面有一个

1
0x1dabd3bb8e99101030cd7094eb15dd525cb0f02065694604071c2a8b10228f30cc12d08fc9caa8d97c65ff481

似乎是 $n$ 的一个因子，

且已经有了分解

1
2
3
11
37517726695590864161261967849116722975727713562769161
41223455646589331474862018682296591762663841134030283

注意到公钥文件里面有四个 *，是被“污染”的 $n$，

这里一个想法是爆破一下，64**4 的复杂度，还好。但是好像最后也没结果。

然后用一用非预期（如果 $flag$ 比较小的话），尝试在“子剩余系“下解密

1
2
3
4
5
6
7
8
9
10
11
12
from Crypto.Util.number import *                                                                                  
p = 37517726695590864161261967849116722975727713562769161
q = 41223455646589331474862018682296591762663841134030283
N = p*q
phi = (p-1)*(q-1)
e = 0x10001
d = pow(e,-1,phi)
enc = 17774316754182701043637765672766475504513144507864625935518462040899856505354546178499264702656639970102754546327338873353871389580967004810214134215521924626871944954513679198245322915573598165643628084858678915415521536126034275104881281802618561405075363713125886815998055449593678564456363170087233864817                            
flag = long_to_bytes(pow(enc,d,N))
print(flag) 

# b'CCTF{l34Rn_WorK_bY__Msieve__A5aP}'

成了！

那如果 flag 比较大怎么办？

（PS：

赛后没有被“污染”的公钥文件公布了，发现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
a='''-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQCkRgRCyTcSwlBKmERQV/BHkurT
5QnYz7Rm18OjxuuWT3AhUeqzq7fHISey2NEEtral/jE7v2Dy59DYHoRAAouWQd02
ZYWnvU5mWoYRcpNmHIj8qk+FOtBWcCGzMZ8uxOxaV74vqqerjxyRI14rXZ+QOcNL
/TMM84h0rl/IKqqWsQIDAQAB
-----END PUBLIC KEY-----'''
b = '''-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCB*QKBgQCkRgRCyTcSwlBKmERQV/BHkurS
5QnYz7Rm18OjxuuWT3A*Ueqzq7fHISey2NEEtral/*E7v2Dy59DYHoRAAouWQd03
ZYWnvU5mWoYRcpNmHIj8q*+FOtBWcCGzMZ8uxOxaV74vqqerjxyRI14rXZ+QOcNM
/TMM84h0rl/IKqqWsQIDAQAB
-----END PUBLIC KEY-----'''

for i in range(len(a)):
	if a[i] != b[i]:
		print(i,a[i],b[i])

59 i *
90 T S
111 h *
133 j *
155 2 3
178 k *
220 L M

发现除了 * 处，还有其他地方也不一样，，emmm，不是很懂出题人啥意思。

DORSA

POINTS：450

考点：RSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#!/usr/bin/env python3

from Crypto.Util.number import *
from math import gcd
from flag import FLAG

def keygen(nbit, dbit):
    assert 2*dbit < nbit
    while True:
        u, v = getRandomNBitInteger(dbit), getRandomNBitInteger(nbit // 2 - dbit)
        p = u * v + 1
        if isPrime(p):
            while True:
                x, y = getRandomNBitInteger(dbit), getRandomNBitInteger(nbit // 2 - dbit)
                q = u * y + 1
                r = x * y + 1
                if isPrime(q) and isPrime(r):
                    while True:
                        e = getRandomNBitInteger(dbit)
                        if gcd(e, u * v * x * y) == 1:
                            phi = (p - 1) * (r - 1)
                            d = inverse(e, phi)
                            k = (e * d - 1) // phi
                            s = k * v + 1
                            if isPrime(s):
                                n_1, n_2 = p * r, q * s
                                return (e, n_1, n_2)

def encrypt(msg, pubkey):
    e, n = pubkey
    return pow(msg, e, n)

nbit, dbit = 1024, 256

e, n_1, n_2 = keygen(nbit, dbit)

FLAG = int(FLAG.encode("utf-8").hex(), 16)

c_1 = encrypt(FLAG, (e, n_1))
c_2 = encrypt(FLAG, (e, n_2))

print('e =', e)
print('n_1 =', n_1)
print('n_2 =', n_2)

print('enc_1 =', c_1)
print('enc_2 =', c_2)

e = 93546309251892226642049894791252717018125687269405277037147228107955818581561
n_1 = 36029694445217181240393229507657783589129565545215936055029374536597763899498239088343814109348783168014524786101104703066635008905663623795923908443470553241615761261684865762093341375627893251064284854550683090289244326428531870185742069661263695374185944997371146406463061296320874619629222702687248540071
n_2 = 29134539279166202870481433991757912690660276008269248696385264141132377632327390980628416297352239920763325399042209616477793917805265376055304289306413455729727703925501462290572634062308443398552450358737592917313872419229567573520052505381346160569747085965505651160232449527272950276802013654376796886259
enc_1 = 4813040476692112428960203236505134262932847510883271236506625270058300562795805807782456070685691385308836073520689109428865518252680199235110968732898751775587988437458034082901889466177544997152415874520654011643506344411457385571604433702808353149867689652828145581610443408094349456455069225005453663702
enc_2 = 2343495138227787186038297737188675404905958193034177306901338927852369293111504476511643406288086128052687530514221084370875813121224208277081997620232397406702129186720714924945365815390097094777447898550641598266559194167236350546060073098778187884380074317656022294673766005856076112637129916520217379601

根据 题目，我们有
$$
p=uv+1,q=vy+1,r=xy+1,s=kv+1，\phi=(p-1)(r-1)=uvxy,ed\equiv 1\pmod \phi,k=(ed-1)/\phi
$$
其中 $e.nbits \approx 256$

注意到
$$
\frac{n_2}{n_1} = \frac{qs}{pr}=\frac{(uy+1)(kv+1)}{(uv+1)(xy+1)}\approx\frac{uykv}{uvxy}=\frac{k}{x}
$$
所以 $k,x$ 有可能会在 $n2,n1$ 的连分数上（具体的关系没有推，做题的时候可以本地测几组数据）

（这里假设 $gcd(k,x)=1$ 了，但是也不一定是 1 叭，但也应该不大，可以小爆破一下？）

有了 $k,x$ 后，我们有
$$
k\phi+1 =ed\equiv 0 \pmod e \to \phi \equiv -1 \cdot k^{-1} \pmod e
$$

$$
\phi =uvxy \equiv 0 \pmod x
$$

有这两条同余式，我们能恢复 $\phi$ 大约 1024bit的信息，即 $\phi \pmod {ex}$。

另外
$$
| \phi -n_1|=|(p-1)(r-1)-pr| \approx p+q \le 2^{513}
$$
由于 $ex$ 大约有 $512$ 比特，我们首先设 $\phi’ = \phi % ex + k\cdot ex$，$k$ 值大约使得我们的 $\phi’$ 和 $n_1$ 一个数量级，然后再在小范围爆破一下即可恢复 $\phi$，从而解密获得 $flag$

exp，来自https://blog.cryptohack.org/cryptoctf2021-hard#dorsa

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from tqdm import 
from Crypto.Util.number import *

e = 93546309251892226642049894791252717018125687269405277037147228107955818581561
n_1 = 36029694445217181240393229507657783589129565545215936055029374536597763899498239088343814109348783168014524786101104703066635008905663623795923908443470553241615761261684865762093341375627893251064284854550683090289244326428531870185742069661263695374185944997371146406463061296320874619629222702687248540071
n_2 = 29134539279166202870481433991757912690660276008269248696385264141132377632327390980628416297352239920763325399042209616477793917805265376055304289306413455729727703925501462290572634062308443398552450358737592917313872419229567573520052505381346160569747085965505651160232449527272950276802013654376796886259
enc_1 = 4813040476692112428960203236505134262932847510883271236506625270058300562795805807782456070685691385308836073520689109428865518252680199235110968732898751775587988437458034082901889466177544997152415874520654011643506344411457385571604433702808353149867689652828145581610443408094349456455069225005453663702
enc_2 = 2343495138227787186038297737188675404905958193034177306901338927852369293111504476511643406288086128052687530514221084370875813121224208277081997620232397406702129186720714924945365815390097094777447898550641598266559194167236350546060073098778187884380074317656022294673766005856076112637129916520217379601

c = continued_fraction(Integer(n_2) / Integer(n_1))

for i in tqdm(range(150)):
    k = c.numerator(i)
    x = c.denominator(i)
    if GCD(e, k) != 1:
        continue
    phi_e = inverse(e - k, e)
    phi_ex = crt(phi_e, 0, e, x)
    ex = e * x // GCD(e, x)

    st = phi_ex + (n_1 // ex) * ex - 100 * ex
    for j in range(200):
        if GCD(e, st) != 1:
            st += ex
            continue 
        d_1 = inverse(e, st)
        flag = long_to_bytes(pow(enc_1, d_1, n_1))
        if b"CCTF" in flag:
            print(flag)
        st += ex
        
b'CCTF{__Lattice-Based_atT4cK_on_RSA_V4R1aN75!!!}'

(PS：看这flag，又非预期了似乎。。。。)

POLISH

POINTS：477

考点：RSA，Partial Key Exposure Attack

1
2
3
4
5
6
7
8
9
10
11
12
13
m = bytes_to_long(flag)

e = 65537

n = p * q
  = 40246250034008312612597372763167482121403594640959033279625274444300931999548988739160328671767018778652394885185401059130887869211330599272113849088780129624581674441314938139267245340401649784020787977993123159165051168187958742107

d = 0b1[REDACTED]00001101110000010101000000101110000111101011011101111111000011110101111000100001011100001111011000010101010010111100000011000101000001110001111100001011001100010001100000011100001101101100011101000001010001100000101000001

c = pow(x**2 + m + y, e, n)
  = 28505561807082805875299833176536442119874596699006698476186799206821274572541984841039970225569714867243464764627070206533293573878039612127495688810559746369298640670292301881186317254368892594525084237214035763200412059090430060075

x**2 * (y - 146700196613209180651680280746469710064760660116352037627587109421827052580531) + y**2 * (x - 146700196613209180651680280746469710064760660116352037627587109421827052580531) = 27617741006445293346871979669264566397938197906017433294384347969002810245774095080855953181508639433683134768646569379922750075630984038851158577517435997971553106764846655038664493024213691627948571214899362078353364358736447296943

根据题目，我们已知 $n,d_{lsb}$，和一个丢番图方程。显然获得flag，除了把 RSA 解密，我们还得解这个丢番图方程获取 $x,y$

那么，先看看怎么解这个丢番图方程，我们有
$$
x^2(y-a)+y^2(x-a)=b
$$
我们设 $u=x+y,v=xy$，上式整理一下有
$$
xy(y+x)-a(x^2-y^2)=b
$$
替换后有
$$
uv-a(u^2-2v)=b
$$

$$
(u+2a)v=au^2+b
$$

$$
v=\frac{au^2+b}{u+2a}
$$

$$
v=\frac{au^2+b+2a^2u-2a^2u}{u+2a}=au+\frac{b-2a^2u-4a^3+4a^3}{u+2a}=au-2a^2+\frac{b+4a^3}{u+2a}
$$

可以看到 $u+2a$ 应该是 $b+4a^3$ 的一个因子，所以我们可以尝试一下分解 $b+4a^3$？因为知道 $a$，然后就能获得 $u$ 了。

这时会发现
$$
b+4a^3=n
$$
那么问题又回到分解 $n$ 上来了。

那么这里泄露了私钥 $d$ 的低位，这里尝试用coppersmith对其进行分解

考虑到 $p,q$ 的大小，如果$p,q$ 数量级差不多，平均分了 $n$ 的比特长度，那么除去已知的 $221$ 低位，我们大约还剩 $166$个低位， $2^{166} \le \frac{1}{2}n^{\beta^2-\epsilon}$ ，那么应该选择 $\beta = 0.5,\epsilon=0.034$

但是这里考虑道 $u+2a$ 是 $n$ 的一个因子，$4a^3+b=n$，$a$ 大约为 $n^{\frac{1}{3}}$，$v=xy=\frac{au^2+b}{u+2a}$，如果 $xy$ 的数量级差不多，那么应该 $x,y,u,a,b$ 都大约是 $n^{\frac{1}{3}}$，那么 $p,q$ 应该是 $258+515$ 这样子的分布。于是我们这里使用参数 $\beta=0.33,\epsilon=0.05$

（PS：由于e很大，所以个人PC挺难跑的，这里解题者是使用了20cores的计算机多线程去跑的。。。。）

exp来自：https://blog.cryptohack.org/cryptoctf2021-hard#polish

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# Part 1 : Factorization of n, written by rbtree
# Also, multiprocess the code below with multiple cores for shorter computation time

e = 65537
n = 40246250034008312612597372763167482121403594640959033279625274444300931999548988739160328671767018778652394885185401059130887869211330599272113849088780129624581674441314938139267245340401649784020787977993123159165051168187958742107

mod = 2^221
d_low = 0b00001101110000010101000000101110000111101011011101111111000011110101111000100001011100001111011000010101010010111100000011000101000001110001111100001011001100010001100000011100001101101100011101000001010001100000101000001

def get_p(p_low):
    F.<z> = PolynomialRing(Zmod(n))

    f = mod * z + p_low
    f = f.monic()
    res = f.small_roots(beta=0.33, epsilon=0.05)

    if len(res) > 0:
        print(res)
        return gcd(int(f(res[0])),int(n))
    return None

R.<x> = PolynomialRing(ZZ)
from tqdm import *
for k in tqdm(range(1, e+1)):
    cands = [1]
    f = k * x^2 + (e*d_low - k*n - k - 1) * x + k * n

    cands = [1]
    for i in range(1, 509):
        new_cands = []
        for v in cands:
            if int(f(v)) % 2^(i+1) == 0:
                new_cands.append(v)
            if int(f(v + 2^i)) % 2^(i+1) == 0:
                new_cands.append(v + 2^i)
        
        cands = new_cands
        if len(new_cands) == 0:
            print("break", i)
            break

    #print(k)
    #print(cands)

    ret = None
    for v1 in cands:
        for v2 in cands:
            if v1 * v2 % mod != n % mod:
                continue
            ret = get_p(v1)
            break
        if ret:
            print(ret)

有了 $p,q$ 后，我们获取 $u,v$，因为之前 $u=x+y,v=xy$，解一个方程我们获取 $x,y$，然后就能解密密文得到 $flag$ 了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Part 2 : Calculating the Flag

def inthroot(a, n):
    return a.nth_root(n, truncate_mode=True)[0]

n = 40246250034008312612597372763167482121403594640959033279625274444300931999548988739160328671767018778652394885185401059130887869211330599272113849088780129624581674441314938139267245340401649784020787977993123159165051168187958742107

a = 146700196613209180651680280746469710064760660116352037627587109421827052580531
b = 27617741006445293346871979669264566397938197906017433294384347969002810245774095080855953181508639433683134768646569379922750075630984038851158577517435997971553106764846655038664493024213691627948571214899362078353364358736447296943

assert n == 4 * a * a * a + b

# from rbtree's code with partial exposure attack on d
p = 893797203302975694226187727100454198719976283557332511256329145998133198406753
q = n // p

u = p - 2 * a
v = (a * u * u + b) // (u + 2 * a)
dif = inthroot(Integer(u * u - 4 * v), 2)

x = (u + dif) // 2
y = (u - dif) // 2

e = 65537 

c = 28505561807082805875299833176536442119874596699006698476186799206821274572541984841039970225569714867243464764627070206533293573878039612127495688810559746369298640670292301881186317254368892594525084237214035763200412059090430060075

d = inverse(e, (p-1) * (q-1))

res = pow(c, d, n)

print(long_to_bytes(res - x * x - y))
print(long_to_bytes(res - y * y - x))

flag:CCTF{Par7ial_K3y_Exp0sure_At7ack_0n_L0w_3xP_RSA}

（PS：看这flag，$e$ 也不小啊，是不是放错了，，，，，）

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可联系QQ 643713081，也可以邮件至 643713081@qq.com

赏

文章标题:2021 CryptoCTF

文章字数:19.6k

本文作者:Van1sh

发布时间:2022-08-30, 13:30:00

最后更新:2023-03-07, 18:34:57

原始链接:http://jayxv.github.io/2022/08/30/2021 cryptoctf/

版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

©2020 Van1sh

Built with Hexo and 3-hexo theme

目录
×

喜欢就点赞,疼爱就打赏